Team and Background
why are you the right person / team for this project?
We are SECBIT Labs. We aim to build high-confidence and trustworthy protocol, application, and facilities on the blockchain. We focus on the research of formal verification, practices of zero-knowledge proofs and blockchain security. We have explored the full formal verification for token smart contracts and decentralized exchanges for the first time. We also have designed and implemented the zkPoD, a practical decentralized protocol for data exchange. We reported many buggy smart contracts on Ethereum, including well-known Fomo3D bugs and attack vectors.
Project and Justification
why is this a valuable addition to the Nervos Ecosystem?
We propose zkp-toolkit-ckb, a toolkit empowering the Nervos community with the cutting-edge techniques of zero-knowledge proofs to develop all kinds of decentralized applications. The project is going to bridge the gap of cryptographic engineering between thriving academic research and aspiring dAPPs developers.
Privacy, performance, and security are the three critical pillars for the mass adoption of blockchain technology. Zero-knowledge proof techniques can hopefully help to fix the first two issues without any sacrifice in security. By a zero-knowledge proof system, a prover interacts with a verifier, convinces the verifier that she holds the knowledge of committed data that the verifier desires, but yields no hint on what the secret might be throughout the whole process[1].
Non-interactive zero-knowledge proof (NIZKP) systems[2] are the best tools innately protecting the privacy of personal data or secrecy. Fascinatingly, particular zero-knowledge proof systems of “verifiable computation”, or “computational integrity”, can guarantee the integrity of computation remotely, even on untrusted hardware, by one single tiny piece of proof without leaking any information relevant.
Since proposed by GMR[1] in the mid of 1980s, zero-knowledge proofs had long been topics among few theoretic researchers before the new realm of blockchain was booming. Zero-knowledge proofs can seemingly solve the dilemma of validating data on the blockchain while preserving privacy or anonymity. In 2016, ZCash firstly adopted a general-purpose zero-knowledge proof system – Pinocchio protocol[3] proposed by Parno et al. in 2013 to achieve perfect anonymity and privacy, popularizing the term of “zkSNARK” around blockchain community. In the following years, more and more practices of NIZKP in blockchain have been done in almost every direction of blockchains; for instance, Filecoin utilizes ZKPs for building decentralized storage systems. A new approach, named zk-rollup, aims to improve the scalability of blockchain through ZKPs. Recently, the Loopring team released the third version of the decentralized token-exchange protocol, which maximizes the computation compressing ability of ZKPs such that the performance was boosted up to 10K TPS on Ethereum, comparing with only 20~30 TPS at layer-1. The Matter Labs is also developing a scaling and privacy engine called ZK Sync basing on zk-rollup for Ethereum. Besides, Most Mixers built on Ethereum are powered by ZKPs to provide privacy for users. Recently, AZTEC Protocol launches its privacy network on Ethereum, which is needless to say that ZKPs are the core of it . Another project, Coda protocol, attracts much attention by claiming that using recursive zkSNARKs, they are going to compress the entire blockchain into only 22 kilobytes, a constant blockchain size even for years of transactions history. Our zkPoD project shows that the problem of fair exchange can be solved by using ZKPs, realizing data trading on the blockchain without trusted third parties.
We anticipate that more applications equipped with ZKPs will come out soon to do jobs that we had thought impossible.
Meanwhile, different ZKP schemes have been proposed with different features. Especially in the year 2019, there were Sonic[6], PLONK[7], Halo[8], Libra[9], Spartan, Virgo, Marlin, Fractal, Aurora, Supersonic, Redshift, etc. Their differences range from proving time, verification time, proof size, to security assumptions, etc. The most popular scheme, Groth16[10], however, requires per-circuit trusted-setup, which is a heavyweight ceremony to generate core components, common reference strings, or CRS. Some new schemes are free of trusted-setup, while some allow for updating common reference strings to mitigate the trusting issues during the ceremony.
By analogy, we are currently experiencing a Cambrian Explosion in the field of cryptographic proofs of computational integrity (CI), a subset of which include zero-knowledge proofs. While a couple of years ago, there were about 1–3 new systems a year, the rate has picked up so much that today we are seeing this same amount monthly, if not weekly.
quoted from “A Cambrian Explosion of Crypto Proofs” by Eli Ben-Sasson[5]
We’ve also seen the increasing number of teams adopting the technology of zero-knowledge proofs both in blockchain infrastructures and dApps. Some of these new schemes could have the potentials to accelerate the applications of zero-knowledge proof in blockchain space and help with the privacy and scalability in a better way. However, many of them haven’t got deserved attention from the blockchain community. Worse, the engineering practice didn’t catch up with the academic achievements in some sense. We need more implementations and explorations in this area.
When trying to use zero-knowledge proofs, developers would be facing the following tough problems:
- Problem A: Very few choices of ZKP library
- Problem B: Very few researches of optimizing ZKP applications in production
- Problem C: Very few guidances about developing arithmetic circuits without introducing vulnerabilities
Considering Problem A, we have to admit that developers do not have too many choices on the ZKP schemes currently, and in general they are using the same scheme. The most popular scheme currently is Groth16, and that’s why many applications are all zkSNARKs-based. It, however, has disadvantages, the most noticeable of which is the unavoidable trusted-setup for every circuit. Groth16 isn’t non-malleable and must be used cautiously. Furthermore, the performance of ZKPs can be very different when they are used in different ways. Developers should choose the proper ZKP schemes for different scenes. The expertise is a prerequisite for building a cryptographic library. It isn’t easy! As the most complicated cryptographic protocols ever since, buggy ZKPs would lead to disastrous results. Problem A and B motivates this project to explore more implementations of new ZKP schemes.
Also, it’s not so easy for dApp developers to transform business logic into ZKP statements that are written in unfriendly mathematical languages. Constructing arithmetic circuits from scratch needs both experience and skills. Developers need high-quality and optimized circuit gadgets and building tools. There might be severe security vulnerabilities in circuits like integer overflows. We need to provide better gadget libraries, utilities, and user-friendly scaffolds for ZKP application developers.
The Nervos CKB has been positioned as the fundamental layer-1 blockchain for all kinds of layer-2 protocols. It’s more than clear that the zero-knowledge proof tech is vital for both layer-1 and layer-2 shortly. The zkp-toolkit-ckb could act as a real crypto infrastructure in Nervos Ecosystem. It may help with attracting more developers to build imaginative layer-2 stuff on Nervos.
Technical Specification and Implementation
how will you implement this successfully?
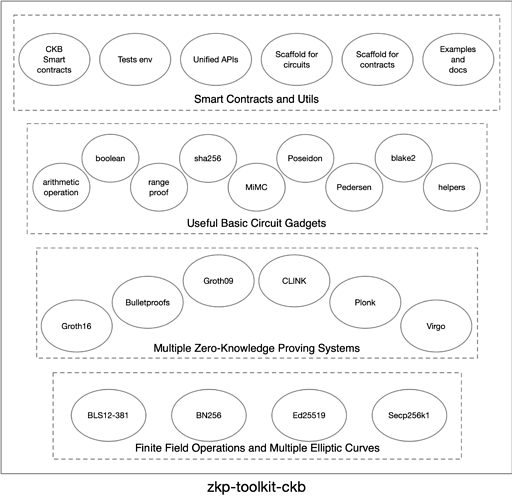
The zkp-toolkit-ckb is going to be a library written mostly in Rust.
In zkp-toolkit-ckb, we will include some of the most used zero-knowledge proving systems, such as Groth16[10] or Bulletproofs[11]. We’ll also investigate many other new proving systems and find out the most suitable ones for the Nervos blockchain. We would implement the most promising ones in zkp-toolkit-ckb finally. The Groth09[12], Plonk[7], and Virgo[13] are on the initial list. It would be possible to move on to better ZKP schemes that emerged in 2020, e.g. those with universal trusted setup or even without the trusted setup would be considered first.
Besides, we would like to implement our newly-developed ZKP scheme, named CLINK. The scheme aims at proving verifiable data processing, optimized for parallel computation on large amounts of data.
The zkp-toolkit-ckb would provide pure rust implementations of these ZKP schemes and try to generalize the programming interface of them for the best developer-friendly experience.
To provide convenience for the most dApp developers, we would implement some useful basic gadgets for the ZKP circuits, such as zkp-friendly hash functions MiMC[14] and Poseidon[15]. Some utils could be made to help with the transformation in different arithmetic circuits so that basic gadgets could be shared for different ZKP schemes.
Lastly but most importantly, zkp-toolkit-ckb is built for the Nervos ecosystem. So this project will try to find out what’s the best fit for Nervos, what’s missing on it, what should be integrated into layer-1 during the whole research and development. We’ll explore the best practice for ZKP applications on Nervos blockchain. The on-chain CKB smart contract libraries to accompany with different ZKP schemes are also important parts in zkp-toolkit-ckb. We could also provide scaffolds for writing and testing ZKP circuits and smart contracts.
There are three main types of security concerns about zkp-toolkit-ckb, (a) theoretical pitfalls, (b) implementation bugs, and (c) circuits vulnerabilities. Part (a) is about the cryptographic assumptions, cryptanalysis, formal proofs of protocols(game proofs, ideal-real proofs, UC proofs). We shall choose the schemes with full formal proofs, and peer-reviewed by academia. The part (b) and (c) can be done by auditing from experts and the community.
“Growing a library” is what we believe to create something really useful, inspired by the motto of “Growing a language” from Guy Steele Jr. The plan we proposed might be adjusted according to the progress of the ZKP community and Nervos community.
A brief overview of ZKP schemes we’re currently interested in.
- Groth16: most popular zkSNARKs, smallest proof size.
- Bulletproofs: Compressible proofs, no trusted-setup, optimized for range proofs.
- Groth09: Lightweight ZKP for linear algebras and matrix operations.
- CLINK: Optimized for parallel data processing, support large-scale data (up to GigaBytes), no trusted-setup.
- Plonk: Universal Trusted-setup, updateable CRS with succinct proof size.
- Virgo: Almost linear proving time, O(log(n)) proof size, no trusted-setup.
As a summary, these items would be the primary targets of zkp-toolkit-ckb.
- porting ZKP schemes: Groth16 and Bulletproofs
- impl. of more schemes including Groth09, Plonk, and Virgo
- impl. of our CLINK scheme which is optimized for parallel computation
- generalize the interface of most schemes for developer-friendly APIs
- impl. of useful gadgets including basic math, Merkle tree, mimc, and Poseidon hash
- utils to make gadgets shareable for many schemes
- impl. of CKB on-chain verifier (smart contract libraries) for corresponding schemes
- scaffolds for easier development of ZKP circuits and contracts
- explore the best practice of ZKP applications on Nervos
Timeline / Roadmap
is the timeline reasonable and justified?
We will take about 12 months to complete this project.
The zkp-toolkit-ckb includes these four main parts:
- underlying libraries of multiple elliptic curves
- ZKP schemes
- basic gadgets
- smart contracts for CKB and utils
We propose four milestones as a roadmap for zkp-toolkit-ckb.
Milestone-I (3 months)
An early runnable version of the toolkit with basic features.
- Finite field operations and elliptic curve
- BN256
- Multiple ZKP schemes
- Groth16*
- bulletproofs**
- Basic circuit gadgets
- basic arithmetic operation
- boolean
- range proof
- Simple on-chain verifier for CKB
Milestone-II (3 months)
Implement more ZKP schemes, improve interface, some demo and examples.
- More ZKP schemes*** and verifiers on CKB-VM.
- Groth09
- Plonk(or Marlin)
- Virgo
- CLINK
- Generalize the interface of most schemes
- Examples of how to use the toolkit
Milestone-III (3 months)
Implement more circuit gadgets, continue to improve the experience for developers, enhance the integration with CKB.
- More useful circuit gadgets
- Hash (SHA256, MiMC, Poseidon, Rescue, Pedersen, and blake2)
- Merkle tree
- Make gadgets shareable for many schemes
- More CKB on-chain verifier (smart contract libraries) for corresponding zkp schemes
Milestone-IV (3 months)
Add support for more curves, scaffolds, and detailed documentation.
- Optimization of finite field operations
- More elliptic curves
- Ed25519
- secp256k1
- BLS12-381
- Nice toolkit APIs easy to use
- Scaffolds for ZKP circuits and contracts development
- Better docs, more tutorials, and rich examples for toolkit usage
Note(*): The implementation of Groth16 will be adapted from Bellman by Sean Bowe (ZCash Team). We will add supports for more curves.
Note(**): Here we will fork the bulletproof lib from Dalek by Oleg Andreev et.al. and add more features such as libsnark R1CS compatibility, non-compressing option.
Note(***): There will be more attractive ZKP schemes added to the list.
References
[1] Goldwasser, Shafi, Silvio Micali, and Charles Rackoff. “The knowledge complexity of interactive proof systems.” SIAM Journal on computing 18.1 (1989): 186-208.
[2] Blum, Manuel, Paul Feldman, and Silvio Micali. “Non-interactive zero-knowledge and its applications.” Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali. 2019. 329-349.
[3] Parno, B., Howell, J., Gentry, C., & Raykova, M. (2013, May). Pinocchio: Nearly practical verifiable computation. In 2013 IEEE Symposium on Security and Privacy (pp. 238-252). IEEE.
[4] Gennaro, R., Gentry, C., Parno, B., & Raykova, M. (2013, May). Quadratic span programs and succinct NIZKs without PCPs. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 626-645). Springer, Berlin, Heidelberg.
[5] Eli Ben-Sasson. A Cambrian Explosion of Crypto Proofs. Jan 08, 2020. A Cambrian Explosion of Crypto Proofs
[6] Maller, Mary, et al. “Sonic: Zero-knowledge SNARKs from linear-size universal and updatable structured reference strings.” Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security. 2019.
[7] Gabizon, Ariel, Zachary J. Williamson, and Oana Ciobotaru. PLONK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge. Cryptology ePrint Archive, Report 2019/953, 2019.
[8] Bowe, Sean, Jack Grigg, and Daira Hopwood. Halo: Recursive Proof Composition without a Trusted Setup. Cryptology ePrint Archive, Report 2019/1021, 2019.
[9] Xie, Tiacheng, et al. “Libra: Succinct zero-knowledge proofs with optimal prover computation.” Annual International Cryptology Conference. Springer, Cham, 2019.
[10] Groth, Jens. “On the size of pairing-based non-interactive arguments.” Annual international conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 2016.
[11] Bünz, B., Bootle, J., Boneh, D., Poelstra, A., Wuille, P. and Maxwell, G., 2018, May. Bulletproofs: Short proofs for confidential transactions and more. In 2018 IEEE Symposium on Security and Privacy (SP) (pp. 315-334). IEEE.
[12] Groth, Jens. “Linear algebra with sub-linear zero-knowledge arguments.” Annual International Cryptology Conference. Springer, Berlin, Heidelberg, 2009.
[13] Zhang, J., Xie, T., Zhang, Y. and Song, D., Transparent Polynomial Delegation and Its Applications to Zero Knowledge Proof. IEEE Symposium on Security and Privacy (S&P) , 2020.
[14] Albrecht, Martin, et al. “MiMC: Efficient encryption and cryptographic hashing with minimal multiplicative complexity.” International Conference on the Theory and Application of Cryptology and Information Security. Springer, Berlin, Heidelberg, 2016.
[15] Grassi L, Kales D, Khovratovich D, Roy A, Rechberger C, Schofnegger M. Starkad and Poseidon: New Hash Functions for Zero Knowledge Proof Systems. IACR Cryptology ePrint Archive. 2019 May 6;2019:458.