构造 zkSNARK 的基本思想和方法——零知识证明引论（二）

[Kelly]

作者： 热爱研究的 Nervos 小伙伴 Cyte

上一篇文章中我们介绍了证明系统以及 ZKP 的定义。从这一篇开始，我们关注如何构造 ZKP。我们只讨论构造通用、简洁、非交互、公开可验证的零知识证明，简称 zkSNARK。本篇会概述构造 zkSNARK 的一些基本原理，以及一些常用的构造 zkSNARK 的工具。而具体的 zkSNARK 构造方案我们会在后续的文章中逐一介绍。

NP 语言的编码

我们要构造可以证明任何 NP 语言的证明系统，那么这个证明系统的代码中并不会“硬编码”任何特定的 NP 语言。当我们想证明 x 属于某个语言 \mathcal{L} 时，除了 $x$，还要将 \mathcal{L} 以某种具体的数据形式输入这个系统。所以，我们要用一个字符串表示一个 NP 语言，也就是对 NP 语言进行编码。

NP 语言是指如果有证据 (Witness) 就能在多项式时间里验证的语言。这里给一个非正式的定义：一个集合 \mathcal{L} 是 NP 语言，如果存在一个多项式时间可计算的确定性函数 $f(\cdot,\cdot)$，使得对任意字符串 $x$，$x\in\mathcal{L}$ 当且仅当存在字符串 w 满足 $f(x,w)=0$。

为了方便，我们把 f(\cdot,\cdot) 叫做这个 NP 语言的标准验证过程，和 ZKP 的验证过程进行区分。

根据上述定义，NP 语言由它的标准验证过程决定，而它的验证过程就是一段计算逻辑。编码 NP 语言，本质上是在寻找一种方式来描述“计算”。图灵机是一种描述计算的方式，还有一种方式是电路。当然，还可以用更高级的编程语言。

如果用高级的编程语言，好处是写程序相对容易，但是在构造 ZKP 时处理起来非常复杂。图灵机的执行过程很简单，为一个图灵机构造 ZKP 就比高级语言容易，但是用图灵机编程的体验就不太友好了。所以，我们要在“容易写程序”和“容易构造 ZKP”之间选择一个平衡点。

一个选择是电路。在用电路写程序方面，已经算是比较成熟了，例如 CPU 以及各种芯片、嵌入式设备、ASIC 矿机等都是电路设计。同时，电路的结构又足够简单，不至于给构造 ZKP 带来太多麻烦。

另一个选项是一个比图灵机稍微复杂一点的模型，叫做随机访问机 (Random Access Machine, RAM) 模型，也是一个不错的平衡点。RAM 模型可以看做一个简单的现代计算机，包括一个 CPU 和一个内存。CPU 支持一些简单的指令集，内存可随机访问。

在表达性方面，RAM 其实比电路更有优势，因为它更接近现代计算机。用 RAM 模型描述计算过程就像用汇编写程序。把高级语言编译成汇编程序，要比编译成电路更方便一些。不过，可能是因为 RAM 模型处理起来比电路要复杂，目前大多数的 zkSNARK 是基于电路模型的，基于 RAM 模型的极少，STARK 是其中的代表，而 STARK 的构造极其复杂。

构造 zkSNARK 时，常用的是算术电路 (Arithmetic Circuit)，而不是硬件中常见的布尔电路。它们的主要区别是：

1. 布尔电路处理的是布尔值，算术电路处理的是有限域 \mathbb{F} 中的元素；
2. 布尔电路的门是逻辑门，算术电路中的门是加法门和乘法门；
3. 算术电路对涉及到代数运算的计算逻辑更友好

算术电路可以进一步转化为数学模型。这个过程叫做算术化 (Arithmetization)。下面介绍一些常见的从电路转化成的数学模型。

R1CS

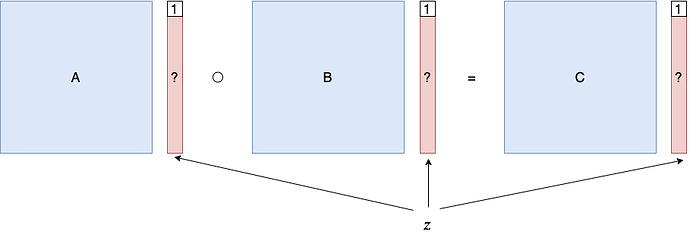
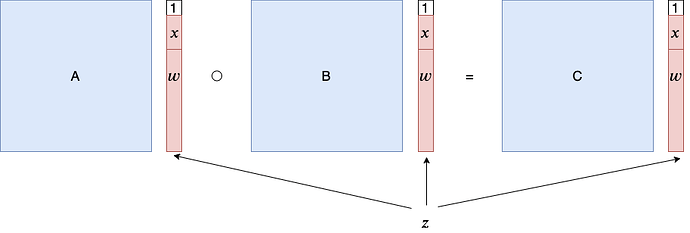
一个 Rank-1 Constraint System (R1CS) 问题由三个方阵 A,B,C\in\mathbb{F}^{n\times n} 来描述。向量 \vec{z}\in\mathbb{F}^{n-1} 是这个 R1CS 问题的解，当且仅当 $A(1,\vec{z})\circ B(1,\vec{z})=C(1,\vec{z})。其中 \circ$ 表示向量的逐项相乘。

把 R1CS 问题的解 \vec{z} 中取固定长度的前缀，记为 $\vec{x}。所有解的前缀 \vec{x} 定义了一个 NP 语言，\vec{z} 中剩下的部分就构成了 \vec{x} 属于这个 NP 语言的证据 \vec{w}$。

通过取不同的矩阵，R1CS 问题可以表示所有 NP 问题。要把一个 NP 问题编码为 R1CS，首先将它的验证过程用算术电路 \mathsf{C} 表示，再进一步转化为 R1CS 问题 $(A,B,C)$。

QAP

R1CS 问题可以继续转化为 Quadratic Arithmetic Program (QAP) 问题。把 R1CS 的解满足的表达式 A(1,\vec{z})\circ B(1,\vec{z})=C(1,\vec{z}) 重新表示成：对任意 $i\in[1,n]$，矩阵 A,B,C 的第 i 行的行向量 (分别记为 \vec{a}_i,\vec{b}_i,\vec{c}_i) 满足 $\langle\vec{a}_i,(1,\vec{z})\rangle\langle\vec{b}_i,(1,\vec{z})\rangle=\langle\vec{c}_i,(1,\vec{z})\rangle$。其中 \langle\cdot,\cdot\rangle 表示内积。

选取 n 个不同的元素 $r_1,\cdots,r_n\in\mathbb{F}$，对任意 $f_1,\cdots,f_n\in\mathbb{F}$，由拉格朗日多项式插值，我们可以得到唯一的 n-1 次多项式 $F(X)$，满足 $F(r_i)=f_i$。

对矩阵 A 的 n 个列分别插值，得到 n 个多项式，组成一个多项式向量 $\vec{A}(X)=(A_1(X),A_2(X),\cdots,A_n(X))$。容易验证，将这个多项式对 r_i 求值会得到 A 的第 i 个行向量，即 $\vec{A}(r_i)=\vec{a}_i$。类似地插值得到多项式向量 $\vec{B}(X),\vec{C}(X)。于是我们有：\vec{z}$ 是 R1CS 的一个解，当且仅当对任何 $i\in[1,n]， \langle (1,\vec{z}),\vec{A}(r_i)\rangle \langle (1,\vec{z}),\vec{B}(r_i)\rangle = \langle (1,\vec{z}),\vec{C}(r_i)\rangle$。

设多项式

F(X)=\left(A_1(X)+\sum_{i=2}^n z_i A_i(X)\right)\left(B_1(X)+\sum_{i=2}^n z_i B_i(X)\right)-\left(C_1(X)+\sum_{i=2}^n z_i C_i(X)\right)

那么，上面的条件又等价于：$F(r_i)=0$ 对所有 i\in[1,n] 成立。令多项式 $T(X)=\prod_{i=1}^{n} (X-r_i)$，则该条件又等价于多项式 T(X) 整除 $F(X)$。

综上所述，一个 QAP 问题是一个四元组 $(\vec{A}(X),\vec{B}(X),\vec{C}(X),T(X))，一个向量 \vec{z}\in\mathbb{F}^{n-1}$ 为 QAP 问题的解，当且仅当存在多项式 H(X) 使得

T(X)H(X)=\left(A_1(X)+\sum_{i=2}^n z_i A_i(X)\right)\left(B_1(X)+\sum_{i=2}^n z_i B_i(X)\right)-\left(C_1(X)+\sum_{i=2}^n z_i C_i(X)\right)

Hadamard 乘积问题

一个 Hadamard 乘积关系由三个矩阵 $M_1,M_2,M_3\in\mathbb{F}^{m\times n}和一个向量 \vec{m}\in\mathbb{F}^m$ 组成。一个向量 \vec{x}\in\mathbb{F}^m 和一对向量 \vec{w}_1,\vec{w}_2\in\mathbb{F}^n 满足 Hadamard 乘积关系，当且仅当 $\vec{x}=M_1\vec{w}_1+M_2\vec{w}_2+M_3(\vec{w}_1\circ\vec{w}_2)+\vec{m}$。

所有存在可能满足 Hadamard 乘积关系的 \vec{x} 构成一个 NP 语言。通过选择不同的矩阵 $M_1,M_2,M_3\in\mathbb{F}^{m\times n}和向量 \vec{m}\in\mathbb{F}^m$，Hadamard 乘积问题可以等价于每个 NP 问题。

下面总结一下现有的 zkSNARK 使用的计算模型：

1. QAP：主要是以 Groth16 方案为代表的一系列基于双线性对的 zkSNARK 在用
2. Hadamard 关系：使用它的方案包括 BulletProof、Sonic
3. R1CS：几乎所有基于电路的 zkSNARK 都用到了 R1CS，如 Groth16、Marlin、Spartan、Fractal、Aurora
4. 分层电路：GKR、Libra 是基于分层电路的
5. RAM：STARK 是基于 RAM 做的，其实也进行了算术化，构造了一个叫做 AIR 的数学问题，然后经过非常复杂的转换得到一个叫 ACSP 的问题
6. 其他：例如 PLONK 等一些 zkSNARK 都是自己搞了一个算术化方案。我们在后续文章中讲对应的 zkSNARK 方案时再做介绍。

实现简洁性

我们刚刚讲到，NP 问题有一个标准的验证过程。相比于这个标准验证，zkSNARK 有两点优势：

1. 零知识性 (ZK)：标准验证需要用到证据，而 zkSNARK 验证不需要，而且 zkSNARK 证明不泄露任何信息
2. 简洁性 (Succinct)：有两点要求
   a) zkSNARK 证明比证据更小
   b) 且/或 Verifier 验证 zkSNAKR 证明比标准验证更快

这两个优势单独拿出来都是很有意义的。ZK 的意义就不用说了。即使只有简洁性，也就是 SNARK (而非 zkSNARK)，也有一些很重要的应用场景，比如说代理计算。例如，一台手机可以借助云服务器进行大量计算，而只需在本地进行少量的计算就可以验证计算结果。这个场景中云服务器并不需要隐私，也就不需要 ZK，但是需要简洁性。

注意到，简洁性的两个要求中，在“验证更快”这一点上，存在一个天然的障碍：上文提到，通用的 zkSNARK 系统中没有包含任何 NP 语言的信息，Verifier 要验证一个 NP 语言，就要把这个 NP 语言的编码输入进来，不妨记为 $C$。$C$ 需要包含完整的计算过程，那么 C 的规模其实和计算量是相当的。那么，Verifier 光是把 C 读完，就已经比这个 NP 语言的标准验证更慢了。

这个问题有两种解决方式：

1. 假设 NP 语言的标准验证可以用很短的信息来描述。一般的电路是做不到的，因为电路大小和计算量相当。而用图灵机、RAM 或高级语言，则有可能用很少的信息描述很大的计算量，关键原因是代码可以复用。例如，高级语言代码中一个简单的循环，写下来可能不超过 100 字节，代表的计算量可能要大得多。这样的计算过程叫做“均匀 (Uniform)”计算，因为大部分计算是在执行相似的逻辑。但是，如果有均匀计算的限制，就会把一大部分 NP 语言排除在外。
2. 对 C 进行预处理。把 C 压缩成一个很小的字符串，不妨记为 $c$。Verifier 只输入 $c$。当然，这样一来 Verifier 没有直接接触到需要验证的计算过程，需要一些密码学工具来防止 Prover 作恶。例如，$c$ 可以是 C 的密码学承诺。

本质上，这两个解决方式是相通的，也就是对 C 进行压缩。如果 C 代表的是均匀计算，就可以无损压缩，否则就只能用密码学工具来压缩。

理想模型

我们的目标是构造 zkSNARK。在我们的目标场景中，Prover 只需要发送一个简短的证明字符串给 Verifier，而 Verifier 不需要给 Prover 发送任何消息。

直接构造一个满足这个场景的 zkSNARK 可能会很困难。一个更灵活的方式是在先在理想模型下构造证明系统，然后用一个通用的转换，把这个只能在理想场景下的系统转化成现实场景中可以工作的 zkSNARK。

理想模型中，就是指这个模型用到了场景中并不存在的功能，叫做理想功能。理想功能的存在使得构造证明更加方便。构造好之后，使用密码学工具模拟这个不存在的功能，以实现这个理想模型。

下图是 ZKP 常用的理想模型，以及它们之间的转换关系。接下来我们会一一介绍这些模型以及它们之间的转换的具体实现。

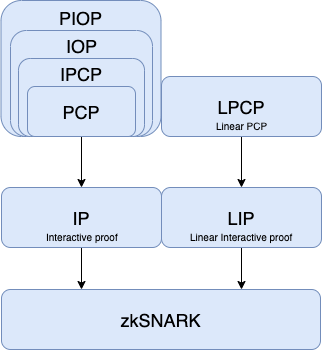
IP

我们在上一篇文章中介绍了交互式证明系统。站在 zkSNARK 的场景看，交互系统就是一个理想模型，因为它提供了一个场景中不存在的理想功能，即 Verifier 可以向 Prover 发送消息。

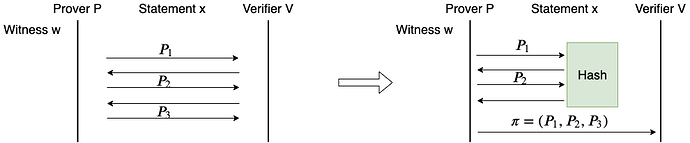
我们已经详细讲过交互式证明系统，这里不再重复，直接讲从交互系统到非交互系统的转换。假如我们已经有了一个交互系统，包括两个算法 \mathcal{P}_{\mathsf{IP}} 和 $\mathcal{V}{\mathsf{IP}}，分别是 Prover 和 Verifier 的算法。现在要构造非交互系统的两个算法 \mathcal{P}{\mathsf{zkSNARK}} 和 \mathcal{V}{\mathsf{zkSNARK}}。核心思想是，让 Prover 在自己的脑海中虚拟出一个 Verifier。\mathcal{P}{\mathsf{zkSNARK}} 调用 \mathcal{P}{\mathsf{IP}} 完成全部的计算，只有在需要 Verifier 消息时，才调用虚拟的 Verifier 产生一条 Verifier 消息。\mathcal{P}{\mathsf{zkSNARK}} 独自执行完成整个交互系统，然后构造一个证明字符串，发送给 \mathcal{V}{\mathsf{zkSNARK}}。\mathcal{V}{\mathsf{zkSNARK}} 根据这个证明字符串，精确恢复 \mathcal{P}{\mathsf{zkSNARK}} 自导自演的交互过程，然后按照 \mathcal{V}{\mathsf{IP}}$ 的逻辑验证这个过程。

我们只考虑公开随机数的证明的转换。公开随机数的证明是指，Verifier 的所有消息都是均匀随机字符串。此时 \mathcal{P}_{\mathsf{zkSNARK}} 可以使用哈希函数 \mathsf{Hash} 来模拟 Verifier 消息。具体做法如下：

1. \mathcal{P}_{\mathsf{zkSNARK}} 初始化 T 为空字符串
2. \mathcal{P}_{\mathsf{zkSNARK}} 执行 \mathcal{P}_{\mathsf{IP}} 的逻辑。每当 \mathcal{P}_{\mathsf{IP}} 需要发送消息时，$\mathcal{P}_{\mathsf{zkSNARK}}$ 将要发送消息添加到 T 上
3. 每当 \mathcal{P}_{\mathsf{IP}} 需要 Verifier 消息时，$\mathcal{P}_{\mathsf{zkSNARK}} 计算 \mathsf{Hash}(T)$ 作为这一步的 Verifier 消息
4. \mathcal{P}_{\mathsf{IP}} 的逻辑执行结束后，$T$ 包含了全部的 Prover 消息
5. \mathcal{P}_{\mathsf{zkSNARK}} 把 T 作为证明字符串发送给 \mathcal{V}_{\mathsf{zkSNARK}}
6. \mathcal{V}_{\mathsf{zkSNARK}} 调用 \mathsf{Hash} 从 T 计算出所有的 Verifier 消息，从而恢复出完整的交互流程
7. \mathcal{V}_{\mathsf{zkSNARK}} 按照 \mathcal{V}_{\mathsf{IP}} 的逻辑验证这个交互流程

上述方法就叫做 Fiat-Shamir 变换。Fiat-Shamir 变换只能将公开随机数的交互证明转化为非交互证明，所以，接下来的理想模型中，只能考虑构造公开随机数的 ZKP。

PCP

Babai 等人在 1991 年提出了随机可查证明 (Probabilistically Checkable Proof, PCP)。在 PCP 模型中，Prover 构造一个证明字符串，叫做 PCP 证明。PCP 证明的长度可以非常长，远远超过 Verifier 的计算能力。所以，Prover 不会直接把 PCP 证明发送给 Verifier，而是向 Verifier 发送一个预言机 (Oracle)，叫做 PCP 预言机。Verifier 可以随意查询 PCP 预言机，获取 PCP 字符串任意位置的比特。

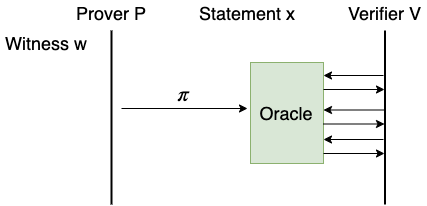
为了理解 IP 和 PCP 的关系，我们举一个现实中的例子。我们请上我们熟悉的主人公 Alice 和 Bob。假设 Alice 是一名即将毕业的研究生，Bob 的任务是评审 Alice 的课题是否合格。IP 模型就是答辩，Alice 和 Bob 直接对话，如果 Alice 能成功回答 Bob 的所有提问，Alice 就成功毕业了。而在 PCP 模型中，没有答辩，Alice 只是把毕业论文发给 Bob，而毕业论文超级长，Bob 不可能看完论文，只能在论文中随机挑选几段来读，如果挑的这些段落都没有问题，相互之间逻辑通顺，Bob 就相信 Alice 的课题是合格的。

PCP 预言机提供了这样的功能：它本身很短，传递它只需要很小的通信量；它传递的信息量却很大，通过它可以随机访问一个很长的字符串。显然，真正的 PCP 预言机是不存在的，PCP 是一个理想化的模型。

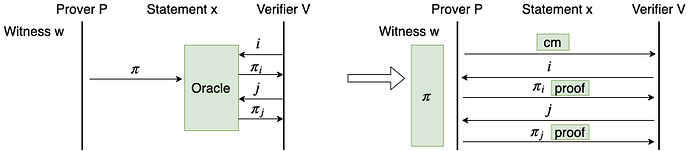
假如我们构造了一个 PCP 模型下的证明系统，包括两个算法 \mathcal{P}_{\mathsf{PCP}} 和 $\mathcal{V}{\mathsf{PCP}}，分别是 Prover 和 Verifier 的算法，可以将它转化为 IP 模型下的证明系统，包括两个算法 \mathcal{P}{\mathsf{IP}} 和 \mathcal{V}_{\mathsf{IP}}。这个转化又要用到哈希函数 \mathsf{Hash}$。

1. \mathcal{P}_{\mathsf{IP}} 按照 \mathcal{P}_{\mathsf{PCP}} 的计算过程生成 PCP 证明字符串 \Pi
2. 当 \mathcal{P}_{\mathsf{IP}} 需要发送 PCP 预言机的时候，$\mathcal{P}_{\mathsf{IP}} 调用 \mathsf{Hash} 在字符串 \Pi$ 上构造一个 Merkle-Tree，并将 Merkle-Tree 的根 \mathsf{rt} 发送给 \mathcal{V}_{\mathsf{IP}}
3. \mathcal{V}_{\mathsf{IP}} 按照 \mathcal{V}_{\mathsf{PCP}} 的逻辑进行验证
4. 每当 \mathcal{V}_{\mathsf{PCP}} 需要访问 PCP 预言机的时候，$\mathcal{V}_{\mathsf{IP}}$ 把要查询的索引 i 发送给 \mathcal{P}_{\mathsf{IP}}
5. \mathcal{P}_{\mathsf{IP}} 将 Merkle-Tree 的第 i 个叶子的值 $v$，连同其 Merkle-Path \mathsf{path} 发送给 \mathcal{V}_{\mathsf{IP}}
6. \mathcal{V}_{\mathsf{IP}} 使用 \mathsf{rt} 和 \mathsf{path} 验证 $v$，如果验证通过，就将 v 作为 PCP 预言机的返回值继续执行 \mathcal{V}_{\mathsf{PCP}} 的逻辑
7. 最后，$\mathcal{V}{\mathsf{IP}} 输出和 \mathcal{V}{\mathsf{PCP}}$ 一样的结果

上述过程中的 Merkle-Tree 可以用更一般的密码学组件向量承诺 (Vector Commitment, VC) 来代替。VC 使得 Prover 可以向 Verifier 发送一个短的字符串 $\mathsf{cm}$，代表对一个向量的承诺，而 Verifier 可以令 Prover 展示出这个向量中的任意位置的值，并提供合法性证明，证明的长度远小于向量的长度。实际上，Merkle-Tree 就是一个简单的 VC 实现。

IPCP

IPCP (Interactive PCP) 模型可以看做 IP 模型和 PCP 模型的相加。在 IPCP 模型中，Prover 向 Verifier 发送了 PCP 预言机后，Prover 和 Verifier 继续进行交互。交互过程中，Verifier 可以不时地访问 PCP 预言机。

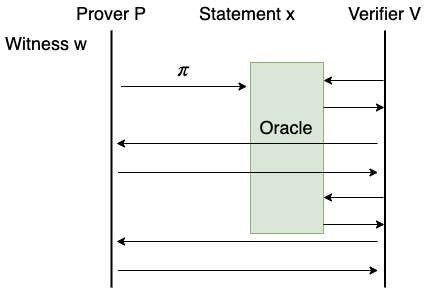
继续使用上一节中 Alice 和 Bob 的例子。如果说 IP 模型是只有答辩，PCP 模型是只有毕业论文，那么 IPCP 模型就是在 Alice 答辩之前把毕业论文发给 Bob。在答辩过程中，Bob 可以一边看毕业论文一边向 Alice 提问。

基于 IPCP 模型构造的证明系统也可以通过 Merkle-Tree 或一般的 VC 方案转化成 IP 模型下的证明系统，过程和 PCP 模型的转换完全一样，区别仅在于，Verifier 在查询 PCP 证明的请求中可能夹杂着普通的交互。

IP 模型和 PCP 模型都可以看做是特殊的 IPCP 模型。其中，IP 模型相当于在 IPCP 模型中 Prover 发送一个空预言机给 Verifier。PCP 模型相当于在 IPCP 中省略掉 Prover 和 Verifier 的对话环节。

IOP

如果说 IPCP 模型是把 IP 和 PCP 模型做加法，那么 IOP (Interactive Oracle Proof) 模型就是把 IP 和 PCP 做乘法。在 IOP 模型中，Verifier 向 Prover 发送消息，而 Prover 则向 Verifier 发送 PCP 预言机。Verifier 可以随意查询 Prover 发过的任何 PCP 预言机。

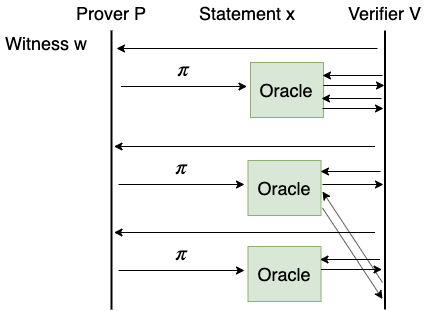
继续使用前面 Alice 和 Bob 的例子来解释 IOP 模型。Alice 把毕业论文发给 Bob，Bob 给 Alice 回复一个简短的评论意见，然后 Alice 再写一篇论文发给 Bob，Bob 再回复，这样来回进行多次。这个过程中，Bob 可以随时阅读 Alice 发给过他的任何一篇论文，当然 Bob 的时间仍然不够，Bob 仍然只能随机选取一小部分阅读。最后，Bob 判断 Alice 的课题是否合格。

和 PCP、IPCP 一样，在 IOP 模型下构造的证明系统也可以类似转化成 IP 模型下的证明系统。

IPCP 模型可以看做特殊的 IOP 模型。在 IPCP 模型中，把对话环节的 Prover 消息都看做一个 PCP 预言机，那么一个 IPCP 模型下的协议就可以看做 IOP 模型下的协议。

PIOP

多项式 IOP (Polynomial IOP, PIOP) 模型是对 IOP 模型的进一步一般化。和 IOP 模型类似，在 PIOP 模型中，Verifier 向 Prover 发送消息，而 Prover 向 Verifier 发送预言机，不过这次不同的是，Prover 发送的是多项式预言机。

一个 PCP 预言机代表了一个固定长度字符串 $s$，而 Verifier 可以向预言机查询 s 的任意位置处的比特 $s[i]$。而一个多项式预言机代表了一个固定次数的多项式 $f(X)$，Verifier 可以向预言机查询 f(X) 在任意 x\in\mathbb{F} 处的取值 $f(x)$。

多项式预言机比 PCP 预言机更强大，因为使用多项式预言机可以实现 PCP 预言机的功能。假如有一个长度为 n 的字符串 $s$，要构造字符串 s 的 PCP 预言机，可以将 s[1],s[2],\cdots,s[n] 插值得到一个 n-1 次多项式 $S(X)$，使得对任意 $i\in[1,n]$，$S(i)=s[i]$。为 S(X) 构造一个多项式预言机，那么这个预言机可以当做 s 的 PCP 预言机来用，因为当查询 i 时，它返回的正是 $S(i)=s[i]$。

因为多项式预言机可以实现 PCP 预言机的功能，IOP 模型可以看做特殊的 PIOP 模型。

把 PIOP 模型下构造的证明系统转化为 IP 模型下的系统，基本思想是和 PCP、IPCP 以及 IOP 的情况一致的，即让 Prover 代替多项式预言机的角色，但是需要的密码学工具就不一样了。简单的 Merkle-Tree 或 VC 是不能模拟多项式预言机的。我们要用到一个更强大的密码工具，叫做多项式承诺 (Polynomial Commitment, PC)。

多项式承诺使得 Prover 可以向 Verifier 发送一个短的字符串 $\mathsf{cm}$，代表对一个多项式 f(X) 的承诺。Verifier 可以向 Prover 请求任意的 $x\in\mathbb{F}$，Prover 返回 f(x) 的值并附带一个证明。根据这个证明和承诺 $\mathsf{cm}$，Verifier 可以验证 Prover 的返回值的正确性。

至此，从 IP 到 PIOP 这条线上的所有模型都介绍完了。过去的几年中，出现了大量基于这些模型构造的 zkSNARK，其中有很多都是无需可信第三方的，Prover 的复杂度大多为拟线性 $O(T\log T)$，Verifier 的复杂度和证明大小多为对数 O(\log T) 或对数的多项式。这里 T 代表 NP 语言的标准验证时间。

接下来我们介绍另外两个模型，LIP 和 LPCP。目前已有的 Verifier 复杂度和证明大小为常数级别的 zkSNARK 都是基于这两个模型构造的。

LIP

在线性 IP (Linear IP, LIP) 模型中，Prover 和 Verifier 进行对话。但是，相比于 IP 模型，增加了一些限制条件：Prover 只能是线性的。

什么是线性的 Prover 呢？首先，Verifier 发给 Prover 的消息只能是 \mathbb{F}^n 中的向量，而 Prover 的消息只能是 Verifier 消息的线性函数。一个向量的线性函数，其实就是在这个向量上乘一个矩阵。所以，在第 i 轮交互中，收到 Verifier 的请求 $\vec{v}_i\in\mathbb{F}^n$，此时 Prover 已经收到了 i 个 Verifier 消息，记这些消息合在一起的向量为 $(\vec{v}_1|\cdots|\vec{v}_i)$，它的长度是 $n\cdot i$。于是，Prover 只能选取一个矩阵 A_i\in\mathbb{F}^{n\cdot i\times k} 并计算 \vec{y}_i=A_i(\vec{v}_1\|\cdots\|\vec{v}_i) 发送给 Verifier。

Prover 计算矩阵 A_i 时，不能用到 Verifier 的请求中的信息，否则 Prover 最终的计算结果就不是线性的了。也就是说，计算 A_i 时只能使用 Setup 信息，陈述 $x$，证据 w 以及 Prover 自己的随机数。因为计算矩阵 A_i 时，Prover 没有用到任何的 Verifier 消息。所以，在和 Verifier 交流之前，Prover 就可以把所有矩阵提前计算好。

因为 LIP 对 Prover 做了很强的限制，它是一个理想模型，现实中并不存在严格遵守约定的 Prover。假如有一个 LIP 模型下的零知识证明系统，现在我们要把它转化成 zkSNARK。转化的思路是，使用密码学手段让 Prover 无法破坏线性的约定。

我们用只支持加法的同态加密 \mathsf{Enc}(\cdot) 来确保 Prover 只能计算 Verifier 消息的线性函数。每当 Verifier 需要发送消息 \vec{v} 时，Verifier 对 \vec{v} 的每一位计算 $c_i=\mathsf{Enc}(v_i)，得到一个密文向量 \vec{c}$。在密文空间中，Prover 只能进行线性运算，而且根据密文无法获知明文。而 Verifier 可以用密钥解开密文 A\vec{c} 得到 $\vec{y}=A\vec{v}$。

使用同态加密 $\mathsf{Enc}(\cdot)，只是把 LIP 模型下的证明系统转化成了 IP 模型下的证明系统。这是一个秘密随机数的证明系统，所以不能对它应用 Fiat-Shamir 变换得到 zkSNARK。要想得到 zkSNARK，需要用到可信第三方 TTP。TTP 采样出所有 \vec{v}_i$ 并加密得到 $\vec{c}_i$，把密文放到 Setup 信息中，然后把密钥删掉。

这样一来，不仅 Prover，连 Verifier 也只能够进行线性运算了。这么一来，这个系统就没多大意义。为了能让 Verifier 做至少一次非线性运算，一个方法就是引入双线性对。双线性对允许对密文做乘法，但是乘法的计算结果是在另外一个密文空间中的，所以不影响安全性。

一个双线性包含以下内容：群 $\mathbb{G}_1,\mathbb{G}_2,\mathbb{G}_T$，其中 \mathbb{G}_1 和 \mathbb{G}_2 的生成元分别为 $g_1,g_2$，以及映射 $e:\mathbb{G}_1\times\mathbb{G}_2\to\mathbb{G}_T$，满足 e(g_1,g_2) 是 \mathbb{G}_T 的生成元，且 $e(\alpha\cdot g_1,\beta\cdot g_2)=\alpha\beta\cdot e(g_1,g_2)$。

即使使用双线性对，Verifier 也只能在验证中使用一次乘法，这对 LIP 模型来说是一个很强的限制。

我们如下构造一个通用的从 LIP 到 zkSNARK 的转换。简便起见，我们假设 LIP 的验证过程中只会用到 \vec{y}_i 和 \vec{v}_i 之间的乘法以及 \vec{v}_i 内部元素之间的乘法。另外假设 Verifier 的消息的计算过程不依赖于 Prover 消息。

给定 LIP 方案 \mathcal{P}_{\mathsf{LIP}} 和 $\mathcal{V}_{\mathsf{LIP}}，以及双线性对 \mathbb{G}_1,\mathbb{G}_2,\mathbb{G}_T,g_1,g_2,e:\mathbb{G}_1\times\mathbb{G}_2\to\mathbb{G}_T$，可以得到如下 zkSNARK 方案：

1. Setup 阶段，由可信第三方执行 $\mathcal{V}，得到 Verifier 消息 \vec{v}_1,\cdots,\vec{v}_m$，计算出 \mathsf{Setup}_P=\mathsf{Setup}_V=(\vec{v}_1\cdot g_1,\cdots\vec{v}_m\cdot g_1,\vec{v}_1\cdot g_2,\cdots,\vec{v}_m\cdot g_2)
2. Prover 按照 \mathcal{P}_{\mathsf{LIP}} 的逻辑，根据输入的 x 和 w 构造矩阵 $A_1,\cdots,A_m$，然后对 i\in[1,m] 计算证明 \vec{y}_i\cdot g_1=A_i(\vec{v}_1,\cdots,\vec{v}_i)\cdot g_1
3. Verifier 调用 \mathcal{V}_{\mathsf{LIP}} 验证 \vec{v}_1,\cdots,\vec{v}_m,\vec{y}_1,\cdots,\vec{y}_m 的合法性。验证过程中，调用映射 e 来计算乘积

LPCP

在线性 PCP (Linear PCP, LPCP) 模型中，Prover 发送一个线性预言机给 Verifier。一个线性预言机代表一个线性函数 $\pi:\mathbb{F}^n\to\mathbb{F}。Verifier 可以随意查询线性预言机，得到 \pi(\vec{v}_1),\cdots,\pi(\vec{v}_m)$，最后根据得到的所有数据做出判断。

LPCP 模型下的证明系统可以由 LIP 模型实现。让 Prover 来充当线性预言机的角色。不过，需要确保 Prover 每次都会用同一个线性函数 $\pi$。因为 Prover 只能使用线性策略，这个转换很简单，完全不用密码学的工具。

给定一个 LPCP 方案 \mathcal{P}_{\mathsf{LPCP}} 和 $\mathcal{V}{\mathsf{LPCP}}，构造如下的 LIP 方案 \mathcal{P}{\mathsf{LIP}} 和 \mathcal{V}_{\mathsf{LIP}}$。

1. \mathcal{P}_{\mathsf{LIP}} 执行 \mathcal{P}_{\mathsf{LPCP}} 生成线性函数 $\pi$。
2. 当 \mathcal{P}_{\mathsf{LPCP}} 需要发送线性预言机时，$\mathcal{P}_{\mathsf{LIP}}$ 什么也不做。
3. \mathcal{V}_{\mathsf{LIP}} 调用 \mathcal{V}_{\mathsf{LPCP}} 生成查询 $\vec{v}_i$。
4. 当 \mathcal{V}_{\mathsf{LPCP}} 需要查询线性预言机时，$\mathcal{V}{\mathsf{LIP}} 将 \vec{v}i$ 发送给 $\mathcal{P}{\mathsf{LIP}}，\mathcal{P}{\mathsf{LIP}}$ 计算 a_i=\pi(\vec{v}_i) 发送给 $\mathcal{V}_{\mathsf{LIP}}$。
5. \mathcal{V}_{\mathsf{LPCP}} 所有的查询结束后，$\mathcal{V}{\mathsf{LIP}} 再额外随机产生 \alpha_1,\cdots,\alpha_m$，并发送 \vec{v}_{m+1}=\sum_{i=1}^m \alpha_i \vec{v}_i 给 $\mathcal{P}{\mathsf{LIP}}$。
6. \mathcal{P}_{\mathsf{LIP}} 计算 a_{m+1}=\pi(\vec{v}_{m+1}) 返回给 $\mathcal{V}_{\mathsf{LIP}}$。
7. \mathcal{V}_{\mathsf{LIP}} 验证 $a_{m+1}=\sum_{i=1}^m \alpha_i a_i$。
8. 最后 \mathcal{V}_{\mathsf{LIP}} 执行 \mathcal{V}_{\mathsf{LPCP}} 的验证逻辑，验证 a_1,\cdots,a_m 是合法的证明过程。

第 5-7 步中验证随机的线性组合，就是用来确保 Prover 每次一定使用相同的 $\pi$。因为在 LIP 模型中，Prover 使用的所有矩阵都是独立于 Verifier 消息的。除非 Prover 在每一步都使用相同的 $\pi$，否则上述第 7 步的验证都大概率不会通过。

小结

本文介绍了构造通用简洁零知识证明 (zkSNARK) 的基本原理和常用工具。首先讨论了 NP 的刻画方式，包括图灵机、电路以及 R1CS 等数学问题。然后讨论了实现简洁性的必要方式：要么假设计算是均匀的，要么使用预处理。最后，理想模型中构造零知识证明比直接在非交互场景中构造更加方便，本文介绍了若干理想模型，以及怎样将理想模型中的零知识证明转化为 zkSNARK。

参考文献

• S. Arora, B. Barak, “Computational Complexity: A Modern Approach”
• L. Babai, L. Fortnow, L. Levin, M. Szegedy, “Checking Computations in Polylogarithmic Time”