作者:热爱研究的 Nervos 小伙伴 Cyte
本文会介绍零知识证明 (ZKP) 的定义,并将零知识证明与 SNARK 和 STARK 这两个概念进行辨析。这些密码学概念随着最近区块链的兴起变得热门起来。但是,这些概念经常会被误解和混用。其实,所有这些概念都属于一个更广义的范畴,叫做证明系统 (Proof System),或者叫做密码学证明 (Cryptographic Proof)。零知识证明和 SNARK、STARK 之间都有交叉的部分,但并不相互包含。它们之间的关系如下图所示。
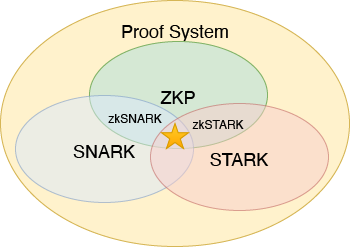
本文将首先介绍证明系统的定义,并讨论证明系统的各类性质,重点讨论“零知识性”、“知识证明”、“简洁性”和“非交互性”。特别的,如果一个证明系统具有“零知识性”,那么它就被称为一个“零知识证明”。最后,文章会讨论 SNARK 和 STARK 的定义并将其进行比较。本文作者是热爱研究的 Nervos 小伙伴 Cyte。
证明系统
一个证明系统 (Proof System) 是一个交互式协议,包含两个参与方 Prover 和 Verifier,以及一个算法 Setup。证明系统的作用是让 Prover 说服 Verifier 相信一件事,我们把这件事叫做一个陈述 (Statement)。
协议开始前,需要由某人调用 Setup 算法。Setup 算法接受一些公共参数作为输入,并输出 Prover 和 Verifier 所需的 Setup 信息,其中 Verifier 获知的信息记为 $\mathsf{Setup}_V$,Prover 获知的信息记为 $\mathsf{Setup}_P$。$\mathsf{Setup}_P$ 和 \mathsf{Setup}_V 的公共部分称为公共参考字符串 (Common Reference String, CRS)。具体由谁、在什么时候调用 Setup 算法,取决于证明系统的设计。
协议一开始,Prover 和 Verifier 同时得到输入陈述 $x$。Prover 相对于 Verifier 必然要有一些额外的优势,例如更强大的计算能力,或者得到了一些额外的输入 $w$。除此之外,Prover 和 Verifier 还分别获知了 \mathsf{Setup}_P 和 $\mathsf{Setup}_V$。Setup 信息获取的时间取决于证明系统的设计。例如,有可能是 Prover 和 Verifier 早就下载好存在各自硬盘里可以反复使用的,也可能是协议开始前当场输入的。
然后 Prover 和 Verifier 开始执行证明系统规定的协议。如果 Prover 和 Verifier 都是诚实的,那么它们都严格遵守协议执行。不过,也有可能某一方是恶意的,没有按照协议规定来执行,此时会发生什么事情,取决于证明系统的安全性。如果两方都是恶意的,它们都不遵守协议,那就和这个证明系统没关系了。
最后,Verifier 输出 accept 或 reject,表示是否相信陈述 $x$。
一个证明系统需要满足两个性质:
- 完整性 (Completeness):如果陈述 x 是正确的,而 Prover 和 Verifier 都遵守这个协议,那么 Verifier 以至少 1-\varepsilon_c 的概率输出 accept,这里 \varepsilon_c 被称为证明系统的完整性误差 (Completeness error)
- 可靠性 (Soundness):如果陈述 x 是不正确的,此时 Prover 必然是不诚实的,而 Verifier 遵守协议,那么任何 Prover 都不能让 Verifier 输出 accept 的概率超过 $\varepsilon_s$,这个 \varepsilon_s 被称为证明系统的可靠性误差 (Soundness error)
这两个要求是使得一个证明系统的最基本的要求。少了哪个要求,我们都可以得到符合条件但完全没用的证明系统。例如,如果我们只要求完整性,那就无论 Prover 做什么,Verifier 永远只输出 accept 就好了;如果只要求可靠性,那就让 Verifier 永远只输出 reject。此外,一般希望 \varepsilon_c 和 \varepsilon_s 都不超过 $1/2$,并且加起来小于 $2/3$,否则这个证明系统误差太大,也近乎无用。
如果将一个证明系统的可靠性只对任何计算能力受限的 Prover 成立,也就是说,计算能力无限的敌手是有可能欺骗 Verifier 的,此时这个证明系统只有计算可靠性 (Computational Soundness),这样的系统又称为 论证系统 (Argument System)。相比之下,对任何 Prover 都安全的可靠性被称为统计可靠性 (Statistical Soundness)。
证明系统的其他性质
一个证明系统还可以满足一些其他(并非必需的)性质
- CRS 模型 (CRS model):如果 Setup 信息是对所有人公开可见的,即 Setup=Setup$_P$=Setup$_V$,称这个证明系统是在 CRS 模型下的
- 交互 (Interactive) / 非交互 (Non-interactive):如果整个交互过程只有 Prover 向 Verifier 发送一条信息,就称这个系统是非交互证明系统;否则这个系统就是交互式证明系统
- 可迁移 (Transferable) / 可抵赖 (Deniable):如果陈述 x 是正确的,并且把交互过程发送给其他 Verifier,也能够让其他 Verifier 相信陈述 x 的正确性,这个证明系统就是可迁移的;否则这个证明系统就是可抵赖的
- 公开可验证 (Public Verifiable) / 特定验证者 (Designated Verifier):如果 Setup$_V$ 是对所有人公开可见的,即任何人都可以成为 Verifier,这个零知识证明系统就是公开可验证的。否则这个系统就是针对特定验证者的
- 公开随机 (Public coin):如果 Verifier 的所有消息的选取都均匀随机且独立于 Prover 的消息,就称这个系统是公开随机的
- 零知识 (Zero-Knowledge):在陈述 x 是正确的情况下,如果除了 x 的正确性,Verifier 无法从交互中获取任何其他“知识”,就称这个系统是零知识的
- 简洁性 (Succinctness):如果这个证明系统是用来证明 NP 语言的,并且证明系统的通信量比证据 w 还要小,那么这个证明系统就具有简洁性
例:证明两个球的颜色不同
Setup 信息:有两个球
陈述 $x$:这两个球颜色不同
Verifier 计算能力受限 (蒙上双眼),Prover 具有正常的视力
- Verifier 左右手各持一个球,展示给 Prover 看。
- Verifier 把双手放到背后,接着 (在心里) 随机抛硬币,如果是正面朝上,就交换左右手里的球,否则不交换。
- Verifier 把球拿出来给 Prover 看。
- Prover 告诉 Verifier 两个球有没有交换。
结果:如果 Prover 猜对了,Verifier 输出 accept,否则 Verifier 输出 reject。
| 性质 | 讨论 |
|---|---|
| 完整性 | 如果两球颜色不同,显然 Prover 一定能以百分之百的概率猜中 Verifier 有没有交换球 |
| 可靠性 | 如果两球颜色相同,那么 Prover 只能盲目猜测,只有 1/2 的概率猜中。这个系统的可靠性误差为 1/2 |
| CRS | 这个证明系统是在 CRS 模型下的,因为 Setup 信息是公开的 |
| 交互性 | 这是个交互系统,因为 Prover 和 Verifier 互相发送的信息超过一条 |
| 可迁移性 | 这个系统是不可迁移的,即可抵赖的。即使 Verifier 把交互过程记录下来展示给其他蒙住眼的人,他们也不能确信两个球颜色不同 |
| 公开可验证性 | 这个系统是公开可验证的,任何 Verifier 都可以和 Prover 进行这个协议 |
| 公开随机性 | 这个系统不是公开随机的,因为 Verifier 发送给 Prover 的信息不是均匀随机的 |
| 零知识性 | 这个系统是零知识的,因为在两个球颜色确实不同的情况下,Prover 的猜测是 Verifier 意料之中的,除了表示陈述 x 的正确性外,没有任何额外知识 |
重要性质
上文中我们给出了证明系统的定义,样例和性质。接下来我们讨论证明系统的几个重要的性质。
零知识性
零知识性用来保护诚实的 Prover 不被恶意的 Verifier 欺骗而泄露证明所需的秘密证据。
上文中已经提到了证明系统的零知识性,将其简单描述为 Verifier 无法从交互中获取任何“知识”。这个描述是不确切的,因为它并没有给出一个严格的判断标准。
零知识性的定义本身是违直觉的:Prover 明明发送了一些比特数据给 Verifier,为什么这个系统会是“零知识”的呢?
实际上,“信息”并不等同于“知识”。如果 Verifier 获取了信息,但获得这些信息并不能让 Verifier 计算出更多结果,或者说这些信息是 Verifier 自己就能够计算出来的,那么 Verifier 就没有获取任何“知识”。
在一个证明系统的执行过程中,Verifier 获得的所有信息包括:$\mathsf{Setup}_V$;Verifier 自己的随机数 $\mathsf{r};Prover 发送给 Verifier 的所有信息 (记为 \mathsf{p})。我们把这些信息称为 Verifier 的“视野”,记为 \mathsf{View}_V=(\mathsf{Setup}_V,\mathsf{r},\mathsf{p})$。这些信息是 Verifier 计算过程中的所有不确定性的来源。确定了这些信息后,其他的一切都可以确定性地计算出来。
注意到,$\mathsf{View}_V$ 是一个随机变量。当 Verifier 与 Prover 执行了证明系统之后,Verifier 会获得这个随机变量的一个样本。如果 Verifier 能在没有 Prover 参与的情况下独自采样 $\mathsf{View}_V$,那么这个系统就是零知识的。
我们把采样 \mathsf{View}_V 这个随机变量的算法叫做模拟器 (Simulator)。根据模拟器工作方式的不同,有如下不同的定义方式:
- 非黑盒模拟器,相对应的零知识性叫做非黑盒零知识。这个零知识的定义允许每个 Verifier 都存在一个“独家定制”的模拟器,这种定义允许模拟器针对不同的 Verifier 的实现细节来定制不同的采样过程。
- 黑盒模拟器,对应的就是黑盒零知识。这个零知识的定义要求存在唯一的模拟器,使得对所有的 Verifier,它都能够采样出 $\mathsf{View}_V$。这个唯一的模拟器不可能知道所有 Verifier 的具体实现细节,所以它只能通过黑盒调用的方式来访问 Verifier。不过,模拟器对 Verifier 具有完全的控制权。模拟器可以决定 Verifier 的随机数 $\mathsf{r},并给 Verifier 输入任何的 Prover 消息或 \mathsf{Setup}_V$。所以,在模拟器的眼里,Verifier 是一个黑盒的确定性算法。
- 如果模拟器只针对诚实 Verifier,对应的是诚实 Verifier 零知识 (Honest Verifier ZK)。因为诚实 Verifier 的行为是完全在预期中的,模拟器自然可以利用这些信息,因此这个模拟器对 Verifier 的访问是非黑盒的。
非黑盒模拟器访问到的信息更多,所以非黑盒零知识性比黑盒零知识性更容易成立。而诚实 Verifier 零知识是最容易实现的。
关于诚实 Verifier 零知识,这里的诚实 Verifier 更准确地说是半诚实 (Semi-Honest) 的,或者说“诚实但好奇的”。这样的 Verifier 表面上会遵守协议,但有可能私下里试图从消息中提取知识。
相比之下,恶意 Verifier 的行为是完全不受限制的。Verifier 可能宕机、发送不符合格式的消息、不按协议规定的分布采样,等等。要证明一个系统对恶意的 Verifier 满足零知识性,就要把所有这些情况都覆盖到。
模拟器是一个随机算法,它的输出值也是一个随机变量,记为 $\mathsf{Sim}_V$。零知识性要求 \mathsf{View}_V 和 \mathsf{Sim}_V 这两个随机变量难以区分。不过,“难以区分”这个词也有很多种版本,由此可以推出零知识证明的多种定义:
- 如果两个随机变量的分布是统计不可区分的,也就是它们的统计距离 (Statistical Distance) 可忽略,就称这个证明系统是统计零知识 (Statistically Zero-Knowledge) 的;如果统计距离就是 0,又叫做完美零知识 (Perfect Zero-Knowledge) 的;
- 如果两个随机变量的分布是计算不可区分的,也就是任何多项式时间的随机敌手都无法区分这两个分布,就称这个证明系统是计算零知识 (Computationally Zero-Knowledge) 的。
注意到,零知识的定义中,只要求对于正确的陈述 $x$,$\mathsf{Sim}_V$ 和 \mathsf{View}_V 的分布难以区分。对于错误的陈述,我们并不关心 Verifier 能够获取什么知识,因为这种情况下 Prover 本身就是不诚实的,没有必要去保护它,或者说,Prover 既然不遵守协议,那我们的协议设计得再好也保护不到它。
不过,虽然 x 是错误的情况下,零知识性对 \mathsf{Sim}_V 的分布不做任何假定,但如果输入错误的 x 采样得到的 \mathsf{Sim}_V 被 Verifier 验证通过的概率和 x 正确的情况下有显著差别的话,我们就可以借此判断 x 的正确性。这就意味着 x 只能来自一个平凡的 NP 语言。所以,对于困难的 NP 问题,把错误的 x 输入给模拟器,得到的 \mathsf{Sim}_V 也能够以一样的概率被验证通过。
这么一来,零知识性和可靠性岂不是矛盾的?换句话说,对于错误的 $x$,Prover 为什么不能调用模拟器来欺骗 Verifier?实际上,Prover 不能控制 Verifier,它也就不能为模拟器提供采样 \mathsf{Sim}_V 所需要的资源。的确,一个恶意的 Prover 可以去调用模拟器,但是这对它来说没用,因为模拟器输出的 \mathsf{Sim}_V 中的 \mathsf{r} 并不是正在与 Prover 交互的 Verifier 的随机数。此外,模拟器输出的 \mathsf{Setup}_V 也可能和 Verifier 收到的 \mathsf{Setup}_V 不同而导致验证不通过。不过,Prover 调起的模拟器无法获取 Verifier 的随机数,这已经足够保证安全性了,所以交互式证明中 \mathsf{Setup}_V 即使是固定常量也没问题。
知识证明
如果要求 Prover 必须“知道”一些信息才能让 Verifier 验证通过,这个系统就被称为知识证明 (Proof of Knowledge)。知识证明可以看做可靠性的加强版。知识证明也有计算意义下的版本,叫做知识论证 (Argument of Knowledge)。
知识证明系统通常是用来证明 NP 语言的。一个 NP 语言是指一个集合 $\mathcal{L}$,使得元素 x 属于 \mathcal{L} 可以由一个证据 w 来证明,即存在一个多项式时间的算法能够判定 w 是否是 x 属于 \mathcal{L} 的合法证据。
普通的证明系统使得 Prover 可以向 Verifier 证明 $x\in\mathcal{L}$。而知识证明系统使得 Prover 可以向 Verifier 证明的不仅是 $x\in\mathcal{L}$,还可以证明 Prover “知道” $w$。也就是说,即使 $x\in\mathcal{L}$,如果 Prover 不知道对应的 $w$,也难以验证通过。
和上一节讨论的零知识性类似,“知识性”也需要严格的定义。一个程序 P “知道”数据 $w$,到底该怎样定义呢?想象一下把这个程序运行在一个虚拟机里,它的随机数是可以由我们随意指定的。它的整个运行过程中,CPU 状态的完整历史记录,以及所有的内存读写操作,都可以由虚拟机记录下来。如果这个程序“知道” $w$,我们总该从这些记录中提取出 w 的信息吧。实际上,这就是提取器 (Extractor) 的一种直观的理解方式。提取器就是一个算法,它能够和被提取的程序同时运行,并能够访问到被提取的程序的内部状态。最后,它可以输出提取的结果。
上面描述的提取器是非黑盒提取器,因为它可以访问被提取程序的内部状态。非黑盒提取器的算法必然要随着被提取程序的不同而变化。所以,一个证明系统是一个知识证明,是这样定义的:“对于任意 Prover $\mathcal{P},存在一个提取器 \mathcal{E},它和 \mathcal{P} 同时执行,并能够访问到 \mathcal{P} 的内部状态。如果 \mathcal{P} 和 \mathcal{V} 交互后 \mathcal{V} 输出 accept,那么 \mathcal{E}$ 就会输出满足条件的 $w$。”
类似于零知识定义中的模拟器,提取器也可以用黑盒的方式定义。提取器无法访问程序的内部状态,但可以调用这个程序,控制这个程序的随机数,并读取这个程序的输出。我们引入这样一个记号 $\mathcal{E}^{\langle\mathcal{P},\mathcal{V}\rangle},表示提取器通过黑盒的方式访问一对 Prover 和 Verifier 的交互过程。黑盒提取器对所有的 Prover 只需要有一个就够了,所以知识性证明就可以如下定义:“存在一个提取器 \mathcal{E},对于任意 Prover \mathcal{P},如果 \mathcal{P} 和 \mathcal{V} 交互后 \mathcal{V} 输出 accept,那么 \mathcal{E}^{\langle\mathcal{P},\mathcal{V}\rangle}$ 就会输出满足条件的 $w$。”
简洁性
用 x 表示一个 NP 语言的实例,$w$ 表示 x 存在语言中的证据。简洁性 (Succinctness) 是指一个证明系统所需的通信量低于 |w| 的线性函数。换句话说,Prover 和 Verifier 执行这个证明系统,比 Prover 直接把 w 发送给 Verifier,还要节省通信带宽。有时候,简洁性还可能要求 Verifier 在证明系统中的计算量要低于验证 $w$。总之,简洁性要求证明系统在效率方面有优势。
我们可能会希望一个简洁证明系统的通信量达到对数级别或更低,即 $O(\log|w|)。然而这样的简洁性要求会带来安全性的损失。因为如果通信量低达对数级别,那么 Prover 的消息组合 \mathsf{p} 所在的整个空间是可以在 \mathsf{poly}(|w|)$ 时间内穷举的。然而,系统的可靠性要求,对于错误的陈述 $x$, Prover 不能找到让 Verifier 验证通过的 $\mathsf{p}$。
假如能够验证通过的 \mathsf{p} 压根不存在,这样确实能够保证可靠性。但这样就可以通过穷举 \mathsf{p} 来判断 x 的合法性,那么 x 就不是一个困难问题,这就排除了一般的 NP 语言。如果我们想要一般的 NP 语言的证明系统,我们必须允许即使对于错误的 $x$,也存在少量的能够验证通过的 $\mathsf{p}$。
这种情况下,我们只能额外引入一个安全参数 $\lambda$,将通信量的大小放宽为 $O(\lambda\log |w|),使得穷举 \mathsf{p}$ 的复杂度达到 $O(2^{\lambda}\mathsf{poly}(|w|)),这样至少实现了计算意义下的可靠性。同时,通信量相对于 |w|$ 仍然是对数级别的,所以满足了简洁性。
综上,对于一般的 NP 语言,(对数级别的) 简洁证明系统只能是论证系统。
非交互性
非交互性 (Non-Interactivity) 是指证明系统的全部交互只有 Prover 向 Verifier 发送的一条消息,这个消息叫做一个证明,记为 $\pi$。非交互性可以带来许多的便利,为证明系统带来更多的应用场景。例如,在区块链系统中,非交互性的零知识证明可以附在交易中,供任何人随时查验,而不需要交易的作者随时在线与验证者交互。
任何 NP 语言都天然具有一个非交互证明协议,也就是 Prover 直接将证据发送给 Verifier,而且这个证明是知识证明。所以,构造一个单纯具有非交互性的证明系统意义不大。非交互性只有和前面讨论的两个性质,即零知识性或简洁性组合起来才有意思。
非交互性 + 零知识
将零知识性和非交互性结合起来,就有了非交互零知识 (Non-Interactive Zero-Knowledge, NIZK)。
我们之前在讨论零知识性时讲到,零知识性之所以和可靠性不矛盾,是因为调用模拟器采样的 \mathsf{Sim}_V 中的 \mathsf{r} 大概率和与 Prover 交互的 Verifier 的随机数不同。但是,对于非交互零知识,我们要重新审视一下这个推理过程。
在交互证明中,一个随机数为 \mathsf{r}_1 的 Verifier 能够验证通过的 Prover 消息 $\mathsf{p},直接搬到随机数为 \mathsf{r}_2$ 的 Verifier 那里就很可能验证不通过了。所以,在交互式证明中,$\mathsf{p} 的正确性不是全局的,而是依赖 \mathsf{r}$ 的。
而在非交互证明中,Prover 没有收到 Verifier 的任何消息,所以 Prover 的计算过程没有用到 Verifier 的随机数 $\mathsf{r}。所以,为了达到证明系统的完整性,诚实的 Prover 输出的 \mathsf{p},对于大部分 Verifier 随机数 \mathsf{r} 都是能验证通过的。所以,非交互证明中的 \mathsf{p} 的正确性是全局的,不依赖任何 \mathsf{r}$。
零知识性要求,Verifier 的视野 \mathsf{View}_V 和模拟器的输出 \mathsf{Sim}_V 不可区分。这意味着,如果单独观察这它们部分分量,它们也是不可区分的。即 \mathsf{View}_V 和 \mathsf{Sim}_V 中的 (\mathsf{Setup}_V,\mathsf{p}) 也是不可区分的。所以,一个恶意的 Prover 可以调用模拟器来输出 $(\mathsf{Setup}_V,\mathsf{p})。这在交互式证明中不成问题,恶意的 Prover 仅仅是得到了关于某个 \mathsf{r} 正确的 \mathsf{p} 罢了。但在非交互证明中,\mathsf{p} 的正确性是不依赖 \mathsf{r}$ 的,就会带来安全问题。
这时候,就要轮到 \mathsf{Setup}_V 发挥作用了。虽然 \mathsf{p} 的正确性不再依赖于 $\mathsf{r},但还是依赖于 \mathsf{Setup}_V$ 的。为了可靠性,我们希望,给定 \mathsf{Setup}_V 和陈述 x 难以计算出能够通过验证的 $\mathsf{p}$。虽然模拟器在给定 x 时可以同时输出一对 $(\mathsf{Setup}_V,\mathsf{p})$,但是难以先计算前者再计算后者。具体是怎样做到这一点的,后续文章中介绍具体方案时会详细讲解。
非交互性 + 简洁性
上文提到,简洁性的证明系统必然是论证系统。结合非交互性,就有了简洁非交互式论证 (Succinct Non-interactive ARGument, SNARG)。实际上,满足 SNARG 定义的系统早在 2000 年就由 Micali 构造出来了,而这个名字是后来才出现的。
如果一个 SNARG 同时是一个知识论证,它就被称为简洁非交互式知识性论证 (Succinct Non-interactive ARgument of Knowledge, SNARK)。SNARK 这个名称由论文 BCCT12 首创,现在已经成为零知识证明领域最热门的概念之一。其实 SNARK 只具有简洁性和非交互性,并不一定具有零知识性。如果有零知识性,应该叫 zkSNARK。
STARK 和 SNARK 辨析
另一个经常和 SNARK 一起提到的概念是 STARK。它和 SNARK 只有一字之差,但有很多不同。下面我们比较一下这两个概念。
共同点:
- 都是知识论证 (ARK),即只有计算意义下的可靠性,且证明是知识性的
区别:
- SNARK 的 “S” 是简洁性 (Succintness),而 STARK 的 “S” 是可扩展性 (Scalability),它在简洁性的基础上还要求 Prover 复杂度至多是拟线性 (Quasi-linear) 的,即 $O(n\log n)$,而 Setup 的计算复杂度最多是对数的
- 透明性 (Transparent):STARK 不需要可信第三方 Setup;而 SNARK 没有这个限制
- 非交互性 (Non-Interactivity):SNARK 一定是非交互的,而 STARK 没有这个限制
可以看出,SNARK 比 STARK 唯一多出的限制就是非交互性。尽管如此,通过后续文章将要介绍的 Fiat-Shamir 变换,STARK 一般都可以转化为非交互证明,转化的结果必然是一个 SNARK。在这种意义上,可以把 STARK 看做 SNARK 的子集。
上述 SNARK 和 STARK 的定义是这两个名词的广义涵义。狭义上,它们分别指代两个具体的构造方案。其中 SNARK 指的是以 Groth16 方案为代表的一系列基于 QAP 和双线性对的 zkSNARK 构造方案。而 STARK 在狭义上就专门指代 Ben-Sasson 等人在 2018 年提出的基于 AIR 和 FRI 的那一个方案。
小结
本文介绍了证明系统的定义,并讨论了证明系统的各类性质,重点讨论了“零知识性”、“知识证明”、“简洁性”和“非交互性”,解释了如何用模拟器来定义零知识性,以及用提取器来定义知识性证明。最后,文章讨论并比较了 SNARK 和 STARK。
参考资料
- Goldreich. Foundations of Cryptography, Volume 1. Basic Tools. 2001.
- ZKProof Community. ZKProof Community Reference. 2019. https://docs.zkproof.org/reference.pdf
- Yehuda Lindell. How To Simulate It – A Tutorial on the Simulation Proof Technique. 2018.
- Eli Ben-Sasson. A Cambrian Explosion of Crypto Proofs. A Cambrian Explosion of Crypto Proofs