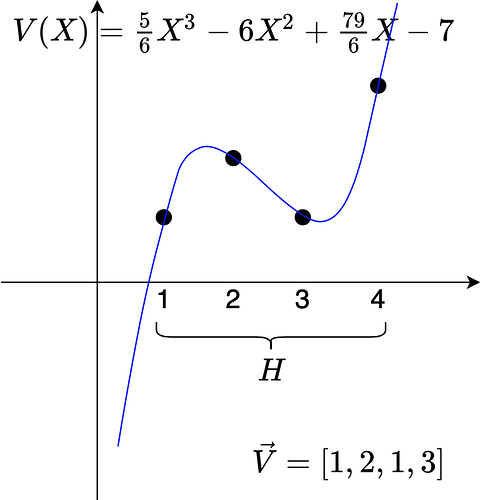作者:热爱研究的 Nervos 小伙伴 Cyte
之前的文章介绍了零知识证明的基础概念以及构造 zkSNARK 的基本思想和方法。从本文开始,我们将逐一介绍目前最热门的 zkSNARK 方案。文章旨在让读者理解这些方案的基本原理。为了方便叙述并容易理解,在叙述方案时,我们会做一些简化处理,重在传达方案的核心思想。
本文介绍的是 Groth16 方案。Groth16 方案,顾名思义,就是 Groth 在 2016 年发表的一篇论文 [Gro16] 中提出的方案。目前为止,Groth16 是在实践中使用最广泛的 zkSNARK (没有之一)。特别一提的,Zcash 目前使用的 zkSNARK 方案就是 Groth16。从性能上,Groth16 的 Verifier 性能是所有 zkSNARK 中最快的,其证明字符串也是最短的。
而 Groth16 的最大缺点就是它需要对每个电路都执行一次可信初始化。
在介绍 Groth16 之前,简单回顾一下 zkSNARK 所要解决的问题。我们称这个问题为“计算验证问题”。
计算验证问题
任何计算都可以描述为一个算术电路。一个算术电路可以对数字进行算术运算。电路由加法门、乘法门以及一些常数门组成,如下图所示。
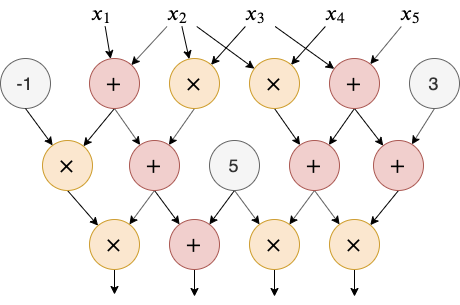
这个例子中的电路包含了 15 个门。这个电路所描述的计算过程需要输入五个数字 x_1 到 $x_5$,输出四个数字。
给定一组输入的数字,需要把这个电路中的每个门都计算一遍,才能计算出这个电路的输出。在这个例子中,如果输入是 $(1,2,3,4,5),则电路的输出为 (-27,14,80,171)$,如下图所示。
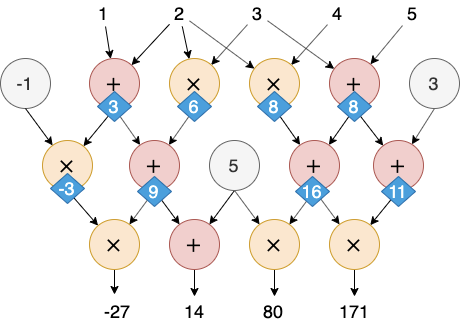
计算验证问题是指,如果一个验证者——不妨叫做 Verifier——只拿到了电路的一组输入和输出,如这个例子中的 (1,2,3,4,5) 和 $(-27,14,80,171)$,它该如何验证这是一对合法的输入和输出呢?最简单粗暴的方法就是把这个输入重新扔进电路算一遍。如果电路很大的话,这个验证方法最大的缺点就是效率问题。
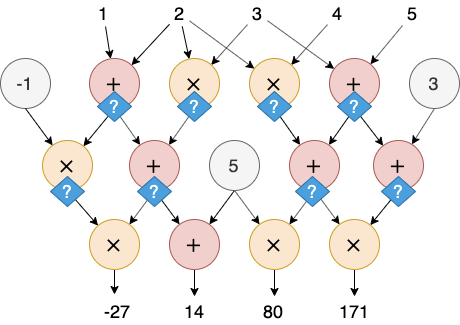
有些场景下,效率还不是唯一的问题。例如,输入可能包含 Verifier 不能知道的秘密信息。假设上例中的 (3,4,5) 是秘密输入,Verifier 只能看到 $(1,2),如下图所示。此时 Verifier 要验证的问题就变成了“是否存在 (?,?,?) 使得电路在输入 (1,2,?,?,?) 的时候的输出是 (-27,14,80,171)$”。这个场景下,即使是简单粗暴的重新计算也不再可行。
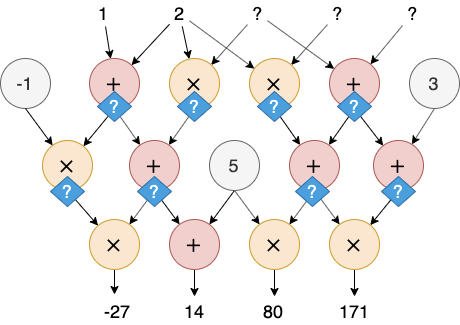
一句话概括计算验证问题:Verifier 能否在不知道秘密输入的情况下,高效地验证计算结果?
从电路到 R1CS 问题
一个 zkSNARK 就是对上述问题的一个解决方案。使用 zkSNARK,一个证明者,叫做 Prover,可以为计算过程生成一个简短的证明字符串。Verifier 读取这个字符串,就可以判断给定的公开输入和输出是否合法。
Groth16 是众多 zkSNARK 构造方案中的一种。接下来,我们介绍 Groth16 是怎么解决计算验证问题的。
首先,我们重新审视一下 Verifier 的任务:我们只知道电路的前两个输入是 $(1,2),我们的目标是要判断是否存在一组合法的秘密输入,使得电路的输出是 (-27,14,80,171)$。如果我们换个角度看这个问题,它其实可以描述为:给一个电路,上面有些空格可以填数字,有些空格已经填上了数字,请问是否存在一种填法,能够同时满足每个门的逻辑?
从这个新的角度,计算验证问题被转换成了一个类似于数独那样的填数字游戏:有一些空格,一部分已经填上,请你填上另外一些空格,满足一些限制条件。
接下来,我们再把这个填数字游戏变成一个数学问题。这个转换其实就是列方程,用到的是小学时就学过的技巧:如果你想要求出一个数字,就把它设为 $x$。只不过,遵循零知识证明领域的规范,这里我们把没有填的空格命名为变量 $w_1,\cdots,w_m$,而把已经知道的空格命名为变量 $x_1,\cdots,x_n$。如下图所示,我们把值已经公开的空格标记为绿色,待求的空格标记为蓝色。
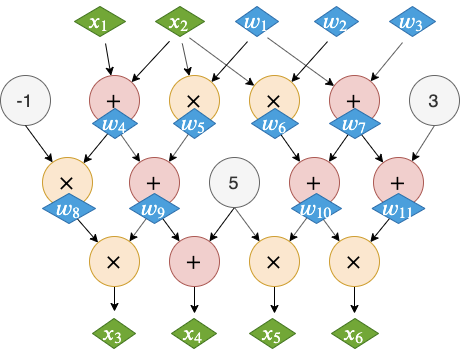
然后,我们为每一个要满足的条件列一个方程。这里,每个要满足的条件其实就是一个门的逻辑:加法门的输出等于两个输入之和,乘法门的输出等于两个输入之积。于是,原来的填空游戏就变成了一个多元方程组。上述例子转化得到的方程组如下
最后,我们对这个方程做一些整理,使得它能够写成矩阵和向量的形式,更加整齐和简洁。我们把每个方程都写成 *=*\times * 的模式。尽管并不是所有方程中都有乘法,但我们可以给没有乘法的式子乘上一个 $1$。于是方程组变成了下面这个样子
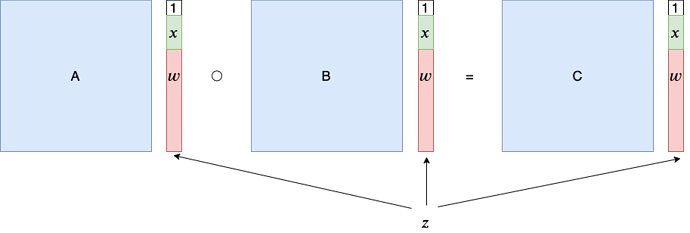
此时,每个 * 中都只包含加法,而不包含乘法。确切地说,每个 * 都是若干变量的相加,有时可能会加上一个常数。更进一步地说,每个 * 都是所有变量 x_1,\cdots,x_n,w_1,\cdots,w_m 和常数 1 的线性组合。于是,设向量 \vec{z}=(1,x_1,x_2,\cdots,w_{11}) 为所有变量以及常数 1 组成的向量。那么,每个 * 都是 \vec{z} 与另外一个常向量的内积。例如,$x_1+x_2=\langle (0,1,1,0,\cdots,0),\vec{z}\rangle$,这里用 \langle\cdot,\cdot\rangle 表示内积。于是,每个方程都可以写成 \langle\vec{c}_i,\vec{z}\rangle=\langle\vec{a}_i,\vec{z}\rangle\times \langle\vec{b}_i,\vec{z}\rangle 的形式,其中 \vec{a}_i, \vec{b}_i 和 \vec{c}_i 是方程组中第 i 个方程对应的三个常向量。
把所有方程合到一起,就得到了原方程组的矩阵表示
其中 A 的行向量就是所有的 $\vec{a}_i$,矩阵 B 和 C 也类似。这里 \circ 表示向量的逐项相乘。这三个矩阵 A,B,C 的值完全取决于电路的结构。
我们把最终得到的这个矩阵向量方程叫做一个 Rank-1 Constraint System (R1CS)。
至于名字中的 “Rank-1” 是怎么来的,如果你感兴趣的话,可以这么理解。每个方程 \langle\vec{c}_i,\vec{z}\rangle=\langle\vec{a}_i,\vec{z}\rangle\times \langle\vec{b}_i,\vec{z}\rangle 的等号右侧可以写成 $\vec{z}^T(\vec{a}_i\vec{b}_i^T)\vec{z},其中 \vec{a}_i\vec{b}_i^T$ 就是一个秩为 1 的矩阵。
总结一下,这一节中我们把计算验证问题转化成了数学问题 R1CS。
在计算验证问题中,Verifier 知道一个电路,拿到公开部分的输入,以及电路的输出,判断它们是否合法。
而在 R1CS 问题中,Verifier 知道三个矩阵 $A,B,C$,并拿到向量 \vec{z} 的一个前缀,判断是否存在一个完整的 $\vec{z}$,满足 $A\vec{z}\circ B\vec{z}=C\vec{z}$。
从 R1CS 问题到 QAP 问题
在零知识证明领域,R1CS 基本上就是电路的代名词。许多 zkSNARK 把 R1CS 问题作为目标问题。不过,大部分 zkSNARK 不会直接对 R1CS 下手,而是把 R1CS 问题继续转化,得到一个等价的多项式问题,再对这个多项式问题设计证明方案。Groth16 也不例外。不同的 zkSNARK 选择的多项式问题各不相同,Groth16 选择的是一个叫做 Quadratic Arithmetic Programming (QAP) 的问题。
这一节中介绍一下怎样把 R1CS 问题转化为等价的 QAP 问题。
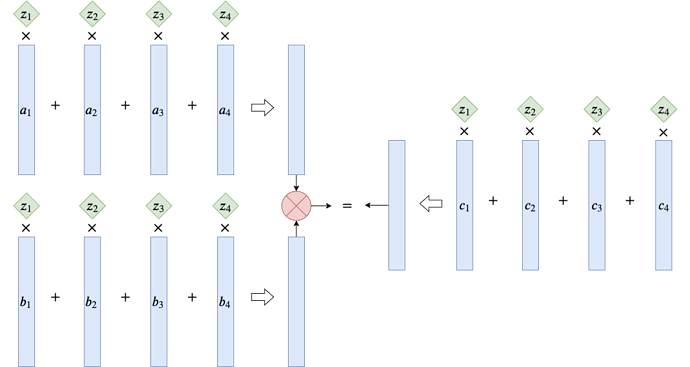
首先,把矩阵和向量的乘积看做对矩阵的列向量的线性组合,这个线性组合的系数由被乘的向量决定。从这个角度看,R1CS 问题就是:给定三个向量集合 (也就是 A,B,C 的列向量),判断是否存在一个线性组合 (也就是 \vec{z}),使得 A,B 的列向量分别组合起来 (也就是 A\vec{z},B\vec{z}),逐项乘积等于 C 的列向量的组合 (也就是 C\vec{z})。如下图所示
然后,我们把这些列向量换成多项式,使得多项式方程和原先的向量方程等价。
把向量转化成多项式的一种方式是使用多项式插值。
多项式插值
多项式插值可以把向量 (例如 \vec{v}=(v_1,\cdots,v_d)) 转化成多项式 $f(X)$,使得 f(X) 在一个点集 (例如 \{r_1,\cdots,r_d\}) 上面的取值刚好是 $\vec{v}$,也就是说 $v_1=f(r_1),\cdots,v_d=f(r_d)$。我们称 f(X) 是 \vec{v} 在插值域 \{r_1,\cdots,r_d\} 上的多项式插值。
给定一个插值域 ${r_1,\cdots,r_d},向量 \vec{v}$ 可以插值为很多不同的多项式。不过,其中次数低于 d 的多项式有且仅有一个。如果不特别说明,当我们说起 \vec{v} 的多项式插值时,默认说的就是这个唯一的次数低于 d 的多项式。
很容易看出,多项式插值是线性的,也就是说,如果 v(X) 和 w(X) 分别是 \vec{v} 和 \vec{w} 的多项式插值,那么对任意的数字 s 和 $t$,$s\cdot v(X)+t\cdot w(X)$ 也是 s\cdot\vec{v}+t\cdot\vec{w} 的线性插值。
QAP 问题
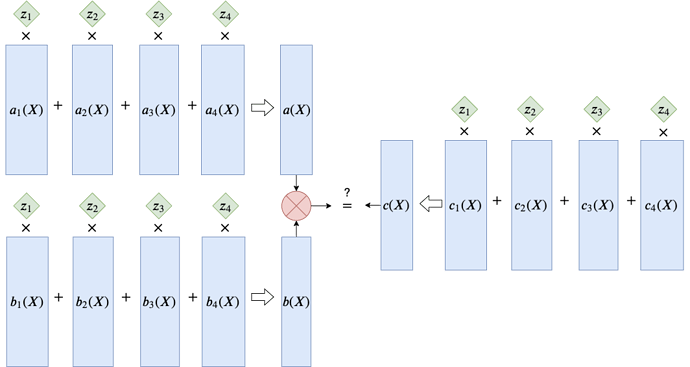
现在,我们直接把 R1CS 矩阵中的列向量换成它们的多项式插值,得到的结果如下图所示。
因为多项式插值是线性的,把各个矩阵的列向量插值得到的多项式经过 \vec{z} 线性组合之后,得到的 a(X),b(X) 和 $c(X)$,就是向量 A\vec{z},B\vec{z} 和 C\vec{z} 各自的多项式插值。
在 R1CS 问题中,我们要求 $A\vec{z}\circ B\vec{z}=C\vec{z}$,这等价于说对插值域中的每个 $r_i\in{r_1,\cdots,r_d}$,$a(r_i)\cdot b(r_i)=c(r_i)$。注意,这并不等于说多项式方程 a(X)\cdot b(X)=c(X) 成立。实际上,因为 a(X)\cdot b(X) 的次数比 c(X) 更高,它们并不相等。我们只能推出,$r_1,\cdots,r_d$ 都是多项式 a(X)\cdot b(X)-c(X) 的根。这等价于多项式 t(X)=(X-r_1)\cdots (X-r_d) 整除 $a(X)\cdot b(X)-c(X)$。
总结一下,一个 QAP 包含如下信息
- 三个多项式集合 \vec{A}(X)=a_1(X),\cdots,a_m(X), \vec{B}=b_1(X),\cdots,b_m(X) 和 $\vec{C}(X)=c_1(X),\cdots,c_m(X)$,其中每个多项式次数都小于 d
- 一个 d 次多项式 t(X)
有了一个 QAP 之后,我们说一个 QAP 问题是指,给定 \vec{z} 的长度为 n 的前缀,判断是否存在 \vec{z} 的完整赋值,使得下面的多项式被 t(X) 整除
我们用一个表格总结一下上文中提到的所有问题。
| 固定信息 | 已知信息 | 秘密信息 | 满足条件 | |
|---|---|---|---|---|
| 电路 | 电路 C | 电路的部分输入以及输出 | 电路所有线路上的值 | 所有门的逻辑 |
| R1CS | 矩阵 A,B,C | \vec{z} 的前缀 | 完整的 \vec{z} | A\vec{z}\circ B\vec{z}=C\vec{z} |
| QAP | 多项式集合 \vec{A}(X),\vec{B}(X),\vec{C}(X) 以及 t(X) | \vec{z} 的前缀 | 完整的 \vec{z} | t(X) 整除由 \vec{A}(X),\vec{B}(X),\vec{C}(X),\vec{z} 计算得到的一个很复杂的多项式 |
为什么要越搞越复杂,把电路问题转化为 QAP 问题呢?一个简单的回答:就是为了引入多项式!多项式是一个强大的工具。多项式的作用,可以理解为一个“杠杆”,或者叫“误差放大器”。如果我们要检查两个长度为 10000 的向量是否相等,一定需要检查 10000 次,哪怕检查过了 9999 个点都是一样的,也不能保证最后一点是相同的。而两个 10000 次的多项式,哪怕非常接近,比如说它们的系数有 9999 个都相同,或者它们在 1,2,\cdots,9999 这些点上的取值都相等,但只要有一个点不同,这两个多项式就截然不同。这意味着,如果在一个很大的范围内,例如 1 到 100000000 当中均匀随机选一个点,两个不同的多项式在这个点上相等的机会只有 $1/10000$。检查两个多项式是否相等,比检查同样规模的向量要快得多,这几乎是所有 zkSNARK 提高 Verifier 效率的根本原理。
为 QAP 问题构造 zkSNARK
QAP 问题就是 Groth16 要用来构造 zkSNARK 的最终问题了。不过,在解释 Groth16 的构造细节之前,我们先准备一些工具。
准备工具
我们假设读者对椭圆曲线群的基本特性和应用有所了解,并采用加法群的记号来描述椭圆曲线群中的点和运算。椭圆曲线群中的元素可以用来表示多项式,并限制 Prover 必须使用给定的多项式来进行线性组合。这正是 QAP 所需要用到的特性。
我们看一下椭圆曲线是怎么用来表示多项式的。
KoE 假设
考虑一对点 P 和 $Q$,如果它们满足 $Q=\alpha P$,我们说 (P,Q) 是一个 \alpha-对。根据离散对数假设,从 (P,Q) 是难以计算出 \alpha 来的。
如果不告诉你 $\alpha$,只告诉你一个 \alpha-对 $(P,Q),请问,你要怎样制造出另一个 \alpha$-对?
一个显而易见的方法是,把 P 和 Q 同时乘上一个整数倍数 $k$,那么 (kP,kQ) 也是一个 \alpha-对。
直觉告诉我们,这是从已知的 \alpha-对产生新的 \alpha-对的唯一方式。换句话说,如果你有能力输出一个 \alpha-对 $(P’,Q’)$,那么,你一定“知道”一个倍数 k 使得 P'=kP 以及 $Q’=kQ$。这个“知道”的含义是,你的计算过程一定“蕴含”了 $k$。如果把你计算 (P',Q') 的过程全部记录下来,这个记录中要么包含了 $k$,要么包含了一些数据,从这些数据中可以轻易地推导出 k 来。
更一般地,如果你已经有了一组 \alpha-对,例如 (P_1,Q_1), (P_2,Q_2), \cdots, $(P_n,Q_n),那么产生一个新的 \alpha$-对的唯一方式,是计算它们的线性组合。也就是说,如果你输出了一个新的 \alpha-对 $(P’,Q’)$,你必须“知道”它们之间的组合系数,即 k_1,\cdots,k_n 使得 P=k_1P_1+\cdots+k_nP_n 以及 $Q=k_1Q_1+\cdots+k_nQ_n$。
然而,上述直觉并不能从离散对数假设严格地证明而来。所以,只能把它作为一个新的安全性假设来用。这个假设就叫做 Knowledge-of-Exponent (KoE) 假设。
KoE 假设怎样应用到 QAP 问题上呢?那就是,KoE 允许我们使用椭圆曲线点来表示多项式,并且迫使 Prover 只能从已知的多项式线性组合产生新的多项式。
首先,怎样用椭圆曲线点表示多项式呢?假设 G 是椭圆曲线群中的一个点,$x$ 和 \alpha 都是秘密的数字。Prover 拿到了 d+1 个 \alpha-对:$(G,\alpha G),(xG,\alpha xG),\cdots,(x^dG,\alpha x^d G),那么,根据 KoE 假设,在 Prover 的计算能力范围内,它所能够产生的所有 \alpha$-对,就是这些已知的 \alpha-对的线性组合,其关于 G 的倍数恰好是 x 的一个 d 次多项式,不妨记为 $f(x)$。
注意到,对于任意多项式 $f(x),它对应的 \alpha$ 对是唯一的,也就是 $(f(x)G,\alpha f(x))。但反过来,对于任何 \alpha$-对 $(P,\alpha P)$,使得 P=f(x)G 的多项式 f(x) 有非常多个。但是,因为 x 是秘密的,Prover 很难找出两个多项式使得它们碰撞到一个 P 上。所以,Prover 最多“知道”一个这样的多项式。这样,至少在计算意义下,一个 \alpha-对能表示的多项式也是唯一的。
其次,KoE 可以迫使 Prover 从现有的多项式组合产生新多项式。原理也是类似的:假如已经有了一些 \beta-对,它们代表了一些多项式 $(a_1(x)G,\beta a_1(x)G),\cdots,(a_m(x)G,\beta a_m(x)G),那么,产生新的 \beta$-对的唯一方式就是对这些多项式线性组合。
不过,到目前为止,我们忽略了两个关键问题:
- 既然 \alpha 是秘密的,我们只能从已有的 \alpha-对产生新的 \alpha-对,那么最开始的 \alpha-对是怎么来的呢?
- 既然 \alpha 是秘密的,我们又该怎样验证一对 (P,Q) 的确是 \alpha-对呢?
关于第一个问题,不幸的是,目前最好的解决办法只能是引入一个可信第三方。这个可信第三方采样一个 $\alpha$,在产生了方案所需的 \alpha-对之后再把 \alpha 忘掉。至于这个第三方到底是不是真的忘了 $\alpha$,那就只能靠信任了。减轻信任问题的方法是使用多方安全计算来模拟这个可信第三方,这不在本文的讨论范围之内。
关于第二个问题,一个解决方法就是双线性配对。
双线性配对
一个双线性配对方案包含三个大小相同的椭圆曲线群 \mathbb{G}_1, \mathbb{G}_2 和 $\mathbb{G}_T$,以及一个能够高效计算的双线性映射: $e:\mathbb{G}_1\times\mathbb{G}_2\to\mathbb{G}_T$。双线性是指对任何 \alpha P\in\mathbb{G}_1,\beta Q\in\mathbb{G}_2,e(\alpha P,\beta Q)=\alpha\beta \cdot e(P,Q).
双线性配对的三个群仅要求大小相同,至于是否是同一个群并没有限制。可能两两不同,某两个相同,甚至三个都相同,由此划分了 I 型,II 型和 III 型等不同种类的双线性配对方案。这些细节不在本文的讨论范围之内。
有了双线性配对,只需要知道 \mathbb{G}_2 中的一个 \alpha-对,例如 $(H,\alpha H),就可以验证 \mathbb{G}_1$ 中的一个点对 (P,Q) 是否是 \alpha-对,而无需知道 $\alpha$,因为只需计算并比较 $e(P,aH)=e(Q,H),这等价于说 (P,Q) 是 \alpha$-对。
现在,我们已经准备好了工具:KoE 假设和双线性配对。接下来,我们就介绍 Groth16 是如何为 QAP 问题构造 zkSNARK 的。
Groth16 方案
回顾一下 QAP 问题:有三个多项式集合 \vec{A}(X), \vec{B}(X) 和 $\vec{C}(X)$,每个都包含 m 个不超过 d-1 次的多项式,此外还有一个 d 次多项式 $t(X)$。QAP 问题的一个解为一个长度 m 的向量 $\vec{z}$。
Prover 知道 QAP 问题的解 $\vec{z}$,而 Verifier 只知道这个解的长为 n 的前缀。Prover 的目标,是向 Verifier 证明,Verifier 所知道的这 n 个数,确实是一个合法的解的前缀。
Groth16 方案包含三个算法:Setup,Prove 和 Verify。最开始,需要由一个可信第三方调用 Setup 算法产生一些公共参数,Prove 和 Verify 算法才能够运行。这个 Setup 算法,对同一个 QAP 只需要调用一次。也就是说,只要 \vec{A}(X),\vec{B}(X),\vec{C}(X) 以及 t(X) 这些多项式不变,产生的参数可以对不同的解$\vec{z} 反复使用。有了公共参数后,Prover 就可以运行 Prove 算法,产生一个证明字符串 \pi$,而 Verifier 可以运行 Verifier 算法验证 \pi 的合法性,并输出 0 或者 1。
Setup
在 Setup 阶段,可信第三方产生一些随机数 \alpha,\beta,\gamma,\delta 和 $x$。设 G 和 H 分别是 \mathbb{G}_1 和 \mathbb{G}_2 的生成元。然后,可信第三方计算如下这些椭圆曲线点:
- 群 \mathbb{G}_1 中的点:
- 群 \mathbb{G}_2 中的点:
注意:这些点中,隐式地包含了许多的 \alpha-对、$\beta$-对、$\delta$-对、$\gamma$-对。
Prove
Prover 采样两个随机数 r 和 $s$,并计算
接下来,Prover 计算三个椭圆曲线点
- 点 A\in\mathbb{G}_1
- 点 B\in\mathbb{G}_2
- 点 C\in\mathbb{G}_1
注意:Prover 并没有显式地产生 \alpha-对、$\beta$-对等等,而是将它们用秘密的随机系数线性组合在一起。其中,$r$ 和 s 这两个随机数是 Prover 用来随机化证明过程的。它们取任何值,证明都是合法的。如果将其取零,上面三个式子中最后一项都会消失,证明依然合法,但不再是零知识的。
Verify
Verifier 首先使用 \vec{z} 的公开前缀计算点 D\in\mathbb{G}_1
拿到证明 (A,B,C) 后,Verifier 验证下式成立
解析
我们简单解释一下上述构造为什么能够工作。至于它为什么是安全的,请感兴趣的读者参阅 [Gro16] 原文。
QAP 问题中,Prover 的目标是证明 t(X) 整除一个多项式 $\left(\sum_{i=1}^m z_i a_i(X)\right)\cdot\left(\sum_{i=1}^m z_i b_i(X)\right)-\left(\sum_{i=1}^m z_i c_i(X)\right)$。这其实等价于证明存在一个商多项式 h(X) 满足
在证明的点 A 中有一项 $\sum_{i=1}^m z_ia_i(X)G$,类似地在点 B 中有一项 $\sum_{i=1}^m z_ib_i(X)H$。当 Verifier 验证证明时,计算 $e(A,B)$,就把这两项乘在了一起,得到了上式左边部分。
点 C 相对复杂一些,包含了 $\frac{1}{\delta}\left(\sum_{i=n+1}^m z_i c_i(X)+h(x)t(x)\right)G$,而 e(C,\delta H) 相当于把 \delta 乘在上面,把原有的 1/\delta 系数给消除了。这就得到了上式的右边部分——但是还缺了 i 从 1 到 n 的那一小块。这一小块由 Verifier 来补上,也就是 $e(D,\gamma H)$。于是上式两边就都补齐并消掉了。
当然,Verifier 的验证式中还包含了许多其他项,但在 Groth 的精心设计下,它们都消掉了。感兴趣的可以自行验证。
小结
本文中,我们解释了 Groth16 这个 zkSNARK 方案的构造原理。我们从算术电路开始,介绍了怎样将计算验证问题转化为 R1CS 问题以及 QAP 问题。然后我们解释了怎样使用 Groth16 方案来证明知道一个 QAP 问题的解。Groth16 方案使用了 KoE 假设以及双线性配对。它的缺点是需要可信第三方进行初始化,而且初始化过程需要对每个电路进行一次。与此同时,Groth16 享有最高效的 Verifier 算法以及最短的证明字符串,使得 Groth16 成为至今仍然应用最广的 zkSNARK 方案。
参考资料
[Gro16] Jen Groth. On the Size of Pairing-based Non-interactive Argument. 2016.