作者∶香橙,Cyberorange
1. 问题背景
1.1 全副本单链困境
传统的单链结构,由于需要所有节点同步所有交易、验证所有交易及存储所有交易,其吞吐能力被所有节点中在网络、计算以及存储最差的一个节点所限制,这构成了单链的瓶颈。
虽然简单提高准入门槛即可提高TPS,并且不妥协可组合性,但这将降低其去中心化与抗审查性,对于某些领域特定且安全需求低的链,如游戏,社交,这种妥协是没问题的,但是对于金融相关,如Defi、大宗交易等,放弃抗审查性缩小了其与传统方案的差别。
1.2 执行分片的复杂性
将各种任务分担给不同的节点,让他们各执行一部分是一个很直觉的扩容方案,几年前的ETH充满乐观地期待Sharding到来的时候,应该想不到如今他们想实现的方案已与当初大不相同。考虑到设计并实施一个真正的分片项目过于复杂和困难,ETH基金会修改了路线并发布了以Rollup为中心的分片路线。
在执行分片中,我们需要应对复杂的跨分片交易,在异步的前提下保持一致性和原子性,我们需要防备适应性攻击的敌手,于是我们需要良好的随机数源,并在不同的委员会组里切来切去,这一切都显得过于困难。
1.3 基于编码与采样
也许我们应该把时间继续往前拨动,在本世纪的交界时间段,P2P文件共享网络正在让信息与资源加速在全球传播,分散且不可靠的P2P节点只存储自己感兴趣的一部分内容,而整个网络本身对外却提供了相对可靠的服务,当然,仅限于热点项目。
也许真正的分片本不该自上而下,由某个调度器安排某些节点验证某些交易,而是由节点自发且随机地验证交易再结合欺诈证明或者有效性证明,这对于区块链来说可能是更好的Sharding。
假如每个区块4MB,以32Byte为一个chunk,全网有1000个节点,每个节点随机从全网抽取2048个chunk即64KB存储,在足够随机且无节点作恶时,每个chunk至少有一个节点存储的概率为 1-(1-\frac{64}{4096})^{1000}=99.99998552644\% ,大概7个9的保证,对于公链来说还是不够。
而且这只是不作恶的情况,因为我们只有获得所有交易才可以构造欺诈证明或者重放至当前状态,如果出块节点恶意扣留了1字节的数据不公布的话,即使有节点发现,也很难证明这件事。
可以让出块者在出块时对数据生成一个MerkleTree,然后每个节点随机抽取数据进行采样,如果获得了数据片和数据片的Merkle Proof则相信抽到的数据片是可用的。
那么对于一个单独的节点,抽取多少数据才能防止有数据不可用呢?
假设一次抽取的chunk数为c,而出现损坏或者被删除的chunk数量为t,令x表示不可用的t块中刚好被抽取到的数量,设不可用数据块中至少有一个包含在被抽取块中的概率为P(X).
根据概率论,可以得到如下推算:
P(X)=P(X\geq 1)=1-P(X=0)=1-\frac{n-t}{n}\times\frac{n-1-t}{n-1}\times...\times\frac{n-c+1-t}{n-c+1}.
由于 \frac{n-i-t}{n-i}\geq\frac{n-i-1-t}{n-i-1} ,有 1-(\frac{n-t}{n})^c\leq PX\leq 1-(\frac{n-c+1-t}{n-c+1})^c 。
概率P(X)表示,如果有t个块不可用,那么在抽取c块后,可以至少发现一个出块人扣留的数据片,从而发现作恶。经过测算,当t是文件的固定占比的一小部分时如 t=mn ,那么c可以用一个独立于总块数的常数块数量,使得P(X)达到确定的概率,即对上面的n求极限,通过夹逼准则,可以得到函数 P(x)=1-(1-m)^c ,这和上面存储的计算是类似的。
通过上述函数,如果不可用数据t占n的1%,那么C抽取460个块和300个块,就可以分别以至少99%和95%的PX概率,发现数据不可用。如果要以99.9%的概率能发现0.1%的数据不可用,则需要抽取6905个数据片。如果要以99.99%的概率能发现0.01%的数据不可用,则需要抽取92099个数据片,依次类推。
可以看到,每个节点需要抽取特别多的数据块,才能以较高概率发现很小的数据丢失,这使得P2P的思路不太实用,但如果我只要能以一定概率保证1/2,甚至1/3的数据是可用的呢?通过纠删码,这是可以做到的。
纠删码可以对数据进行处理,生成校验数据,然后再这些数据内,只要收集了一定阈值的数据块,就可以恢复回原始数据。比如对于(20-10)纠删码,对10个原始数据生成10个校验块,这20个数据块任意10个都可以恢复回原始数据,由此,我只需要保证50%的数据是可用的即可。
在这个前提下,通过计算,每个节点只需要随机抽34个数据块,就可以以99.99999999%的概率发现50%以上的数据不可用,这使得轻节点也可以为链提供安全性。而一旦数据不可用的比例小于50%,我们可以通过纠删码将数据恢复回来。
继续用上面那个例子,假如每个区块4MB,纠删码扩展到8MB,以32Byte为一个chunk,全网有1000个节点,每个节点随机从全网抽取2048个chunk即64KB存储,在足够随机时,至少有一半的chunk在全网存储的概率应该非常接近于1。
1.4 共享安全的模块化区块链
由此,我们可以在波卡或者Cosmos上更进一步,去思考安全的应用链网络应该怎么设计,首先,无论是基于欺诈证明的Optimistic Rollup还是基于有效性证明的zkRollup,它们都需要一个root chain去仲裁或者验证某个Layer2链的状态转换,所以一个root chain是必要的。
如果所有的Layer2链的节点都参与到全局DA层的采样,这些Rollup可以看作是具有共享安全的,由于它们都具有同样的结算层仲裁以及验证,具有同样的数据可用性保证,这些链可以理解为是共享安全的。
对于zkRollup,由于没有挑战期,zkRollup在共享安全的前提下可以互相信任,通过设计原生的通信机制来通信,就像多个执行分片一样。
Optimistic Rollup基于某些组合范式,也可以具有原生的通信机制,比如A链的区块101依赖B链的101块上的某个交易或者状态检查点,如果B链的101块被挑战后逆转了,那么通过B链101块已逆转这个信息,可以逆转A链的区块101,从而保证整个区块链网络的一致性,某些基础设施链可以通过这种插件方式为其他链所用。
当然,除了参与到全局DA层的采样外,Layer2的组合还可以更进一步,也许某些Layer2可以形成一个Group,它们需要质押某种相同代币以参与共识,并共享某些基础模块,比如身份、资产,而最重要的资产、身份相关交易,由所有Group内的节点共同验证,这使得用户可以用一个身份在组内所有Layer2上交互并且保持资产的可组合性。
2. 编码问题
2.1 纠删码
前面我们在采样中使用纠删码,从而让每个节点需要采样的数目维持在一个极低的常量即可保证超高的数据可用性,那么接下来需要讲一些纠删码的基础概念。
假设数据长度为n,我们将数据扩展到 n/r ,并且任意的 qn/r 都能恢复回原数据u,q被称为stopping rate,当q=r时,我们称这种编码是最大距离可分码(maximum distance separable,MDS),这是一种具有最佳容错能力的编码方案。
Reed-Solomon就是一种MDS码,我们可以通过多项式来理解它。
假如我有n个数据片 m_i ,构造一个n-1阶多项式 \phi(x)=\sum_{i=0}^{n-1} a_i^{x_i} ,使得 \phi(i)=m_i ,这样的话,这个曲线将经过 \{i,m_i\}_{i=0}^n 里所有的点,在此基础上再求出 \phi(i+1) ...\phi(2i) ,因为知道 n 个点就可以恢复回一个 n-1 阶的多项式,所以知道 \{i,m_i\}_{i=0}^{2n} 中任意n个点,都可以通过拉格朗日插值或者快速傅里叶变换求出多项式的所有系数,然后恢复出所有的值,当然,为了保证计算的精度,这个多项式是定义在有限域上的,一般是一个伽罗华域,比如 GF(2^8) 。这个方案的 q=r=1/2 。要使得这个方案可用,我们需要寻找一种能将多项式快速从点值表达转换为系数表达的算法,如快速傅立叶变换。
在存储领域的应用中,往往会把这个问题转化为一个有限域上的矩阵运算,其实是把一个高阶多项式转化为方程组,然后矩阵化而来的,以经常使用的范德蒙德矩阵为例。
假如数据存在丢失,如D2和P2丢失。
可以将右边矩阵对应丢失数据的行删掉,求出剩余矩阵的逆矩阵,然后等式两边同乘逆矩阵,就可以通过剩余的数据中把数据都修复回来,所以这种模式需要保证去掉小于等于阈值行的矩阵的子矩阵都是可逆的。
2.2 错误编码证明
但是基于纠删编码的模式还存在一个问题,即出块者可能没有如实对数据进行编码,这样的话,轻节点的采样就不再有意义,因为数据无法恢复。
为了应对这种恶意出块人,需要设计一个错误编码证明,让所有节点知道这个区块的编码错误然后丢弃,但是对于普通的一维纠删码,生成错误编码证明至少需要所有的原数据+一个冗余块,还要加上MerkleProof,即 O(n\log((n)) ,这使得这个方案在最坏情况的通信复杂度比全同步还要差,使得该方案不再实用。但如果我们愿意降低编码效率的话,则可以降低错误编码证明的大小。
2.3 RS码从一维到高维
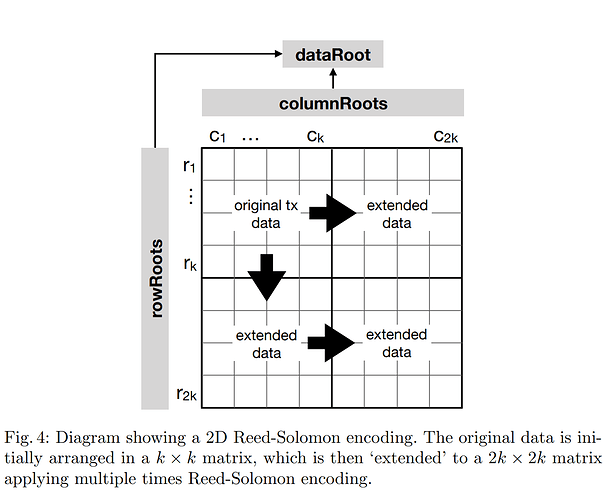
在论文Fraud Proofs: Maximising Light Client Security and Scaling Blockchains with Dishonest Majorities中,提出使用二维乃至多维纠删码对数据进行编码,这相比一维纠删码降低了一定的编码效率,但是错误编码证明也大大降低。
对于二维纠删码,其欺诈证明大小则变成了为 O(\sqrt n\log((\sqrt n)) ,只需要一行或者一列的错误编码证明即可,大大减少了需要的通信开销,但是该方案需要轻节点同步的commitmente则从一个固定的hash,变为所有行+所有列数的哈希值,即 2 \times(2k)^2 个哈希值。
2.4 LDPC
除了高维纠删码外降低错误编码证明外,也有些方案利用LDPC、Polar等纠错码方案。
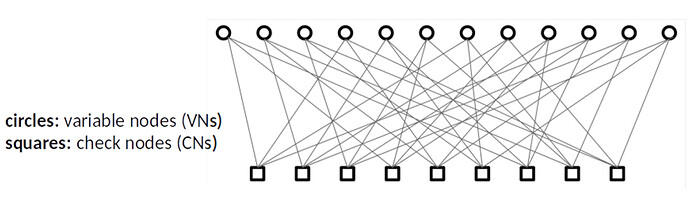
LDPC(Low Density Parity Check Code,低密度奇偶校验码),通过将一些数据片和某个校验数据片XOR后等于零,来生成校验数据,它的编码效率相比RS码低了很多,不具备MDS性质,Coded Merkle Tree就使用了LDPC作为它使用的纠删码算法。
通过上面这个Tanner Graph可以知道,利用LDPC编码,错误编码证明不再需要 qn 的数据参与,而是某个奇偶校验等式涉及的值即可。
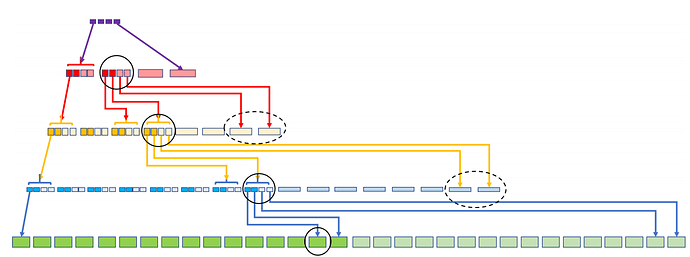
Coded Merkle Tree使用LDPC对Merkle的每一层进行纠删编码,即对于下一层进行纠删编码再哈希得到上一层后,再纠删编码往上,直至根节点。
相比二维纠删码,CMT可以使得通过固定大小的Commitment即可采样所有数据的可用性,并且通过一次采样还可以保证中间层的正确性。
但是LDPC的编码效率较低,在 r=1/4 即冗余数据三倍于原数据时,最多还可能需要 q=0.875 的数据块才能恢复回数据。而且,由于LDPC的stopping rate不可控,需要利用图论算法等工具保证其下限,这提高了其方案的复杂性,而且出块人还可能挑选一个只有极少数数据参与的XOR等式,并隐匿其中一个数据,文中称之为bad code,又需要设计方案来检测。
3. 多项式承诺
3.1 舍弃错误编码证明
在上面的方案中,我们需要权衡错误编码证明的大小和编码效率来设计方案,那有没有可能彻底舍弃错误编码证明,从而使得出块者没法错误编码证明呢?多项式承诺就是这样一种神奇的工具,
由前面我们知道,Reed Solomon是基于多项式的编码方案,那么再结合一个多项式证明方案,先对多项式 \phi(x) 生成一个承诺, Com(\phi(x))=C ,然后存在一个证明机制,对于某个索引Index和其对应的取值value,可以生成一个证明Witness,证明C绑定的多项式在index的取值就是Value。
通过这样一种机制,出块人在出块时可以先对数据进行编码,然后运用多项式承诺得到承诺值,任何节点包括轻节点,都可以通过 (index, value, witness, C) 来验证该点的可用性,同时,有些多项式承诺方案还支持batch verify,即同时证明多个点的取值,只需要一个证明。由于该证明保证抽取的点一定在绑定的多项式上,所以出块人是无法错误编码的,从而规避了错误编码证明的需要。
3.2 KZG Polynomial Commitment
在所有的多项式承诺中,KZG Polynomial Commitment ( Constant-Size Commitments to Polynomials and Their Applications )是各方面属性最好的,它的承诺值是固定大小的,并且证明也是固定大小的,对于多个点值的证明也可以batch成一个证明,但是KZG需要Trust setup,它不是抗量子的,而且公共参数大小随着承诺多项式的最大阶数线性增长。除了kzg以外,还存在别的Polynomial Commitment方案,但在实用性上暂时都不如kzg。
3.2.1 Pairing
KZG使用了Pairing,双线性映射,并基于一些难度假设,比如离散对数:知道 y=g_1 \cdot \alpha 不能反推出 \alpha 的值。
一个典型的非对称双线性映射的定义如下:
假设 G_1 是生成元为 g_1 的循环加法群, G_2 是生成元为 g_2 的循环加法群, G_t 是一个乘法循环群,它们的阶都为p。当映射 e: G_1 \times G_2\rightarrow G_t 满足下面的条件时,称为双线性配对:
- 双线性性质:对于素数域 F_p 的a,b,且 Q_1,Q_2,Q\in G1, R\in G2 ,满足 e(a\cdot Q_1+b\cdot Q_2,R)=e(Q_1,R)^a\cdot e(Q_2,R)^b,\space e(a\cdot Q,b\cdot R)=e(Q,R)^{ab} .
- 非退化性:存在 Q\in G1,R\in G2, e(Q,R)\neq 1 .
- 可计算性:对任意的 Q\in G_1, R\in G_2 ,存在有效的算法计算 e(Q,R) 的值.
3.2.2 Trusted Setup
首先需要构建公共参数,这个可以通过一个分布式的机制来完成,保证私密信息 \alpha 不会泄露。
3.2.3 Commitment
计算多项式 \phi(x) 的承诺,可以通过 C=g_1\cdot{\phi(\alpha)}=\sum_{j=0}^{\deg(\phi)}(g_1\cdot{\alpha^j}\cdot \phi_j) 求得。
3.2.4 Create Witeness
假设需要生成 i 的取值为 \phi(i) 的证明,首先计算出 \psi(x)=\frac{\phi(x)-\phi(i)}{x-i} ,由于这个一定能整除,所以 \psi(x) 的阶应该正好比 phi(x) 小一位,然后计算出 w_i=g_1\cdot{\psi(\alpha)} ,计算方式与计算Commitment类似,并将 w_i 作为证明。
3.2.5 VerifyEval
通过双线性映射,判断 e(C,g_2)=e(w_i,g_2\cdot\alpha-g_2\cdot i))\cdot(g_1^{\phi(i)},g_2) 是否相等。
3.2.6 batch verify
如果我们需要同时对s个点的取值集合 S=(p_1,\phi(p_1)),....,(p_s,\phi(p_s)) 生成证明的话,首先需要对这些点进行拉格朗日插值得到插值多项式 r(x) 。
然后计算 \psi_S(x)=\frac{\phi(x)-r(x)}{\prod_{i\in S}(x-i)} ,由于 r(x) 是通过拉格朗日插值计算出来的,故这个多项式一定能整除。
计算 w_S=g\cdot\psi_s(\alpha) ,即为证明。
通过式子 e(C,g_2)=e(w_S,g_2\cdot\prod_{i\in S}(\alpha-i))\cdot e(g_1\cdot{r(\alpha)},g_2) 来验证证明是否成立。
上面描述的仅是最基础的Kate Polynomial Commitment,后面还有一些改进方案。如下所示:
Efficient polynomial commitment schemes for multiple points and polynomials
fflonk: a Fast-Fourier inspired verifier efficient version of PlonK
3.3 问题
目前对于高阶多项式,利用KZG commitment去承诺会带来问题,首先是公共参数过大的问题,其次是涉及的快速傅立叶变换相关的运算会非常复杂。
所以可以结合一些前面的2D-RS code,由于所有的行和列都可以复用公共参数,使得多项式的阶数能保持在几千这个量级,Vitalik在2D data availability with Kate commitments - Sharding - Ethereum Research中对这个想法进行了论述。
由于本方案中一切都是线性组合的,所以原数据所有行的Commitment可以插值得到所有冗余数据行的Commitment,而不需要拥有冗余数据。所以任何一个节点,知道原数据行的所有Commitment后,可以直接计算出冗余数据的Commitment,相比原来基于MerkleTree的二维纠删码方案,需要所有节点同步的commitment从所有行数加上所有列数,变成了原数据的行数,并且无需欺诈证明。
所有的节点需要同步原数据行的Commitment,这个可以作为一笔交易发送给root chain全同步,从而让所有节点都可获取。
- 普通全节点可以任选一行进行存储并响应针对这一行的DA采样,同时采样自己未存储的那些行与列的数据。
- 轻节点通过commitment采样所有行与列的数据。
- 配置和带宽更高的全节点,可以存储所有数据并响应采样。
- 依赖于承诺数据的应用,只需要请求应用涉及的数据并存储下来即可。
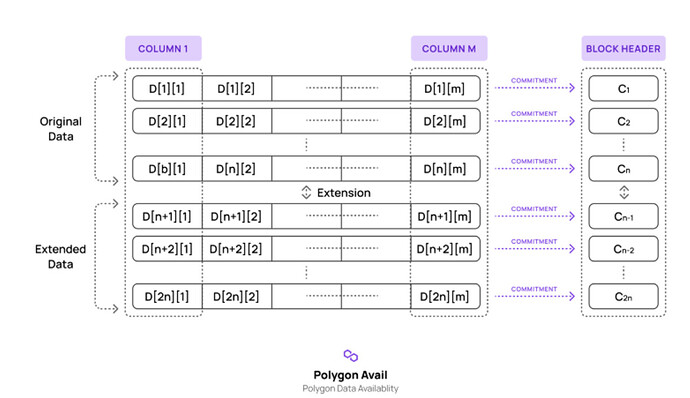
Polygon avail基于这个思路设计,由他们提供的这个图有助于理解这个方案。
4. 信息扩散算法
在一个P2P网络中,还需要设计好的信息扩散算法,保证信息被良好地扩散到全网,这个可以对应bittorrent的做种阶段。
TODO
5. 将DA与Rollup结合
对于zkRollup,可以通过承诺之间的等效性证明( Proof of *equivalence),即Proof的公共参数的承诺与DA层承诺的等效来解决。
对于Optimistic Rollup
-
单轮欺诈证明,可以按照交易顺序在Polynomial Commitment中按照索引顺序铺开,比如索引1号存第一笔交易的原数据和检查点,以此类推;或者读取索引1号的取值,一直往后读,直到某个索引值包含一个特殊停止标识符,这一段数据为第一笔交易的数据,以此类推。
-
多轮欺诈证明,等找到争议的某笔指令,再把对应索引的数据上链以便裁断。
TODO
6. 与CKB的整合可能
6.1 原生DA层
用户可以通过特殊交易格式发布数据,结合NC-MAX,该交易的Commitment应先放置在特定的提交区,然后矿工开始对该交易数据进行采样和选择存储,在经历过某些区块数后,再发送一个确认交易,如果某矿工认为区块内所有交易合法,并且承诺的数据是Available的,则接受区块,否则拒绝。交易可以通过header_deps读取某个区块具有的commitment以在交易内保证数据可用性。
这修改了共识机制,可能会造成安全风险和更多的攻击可能,但如果可以提供一个原生的DA层的话,对于Layer2的发展是很有帮助的。
6.2 侧链DA层
除了原生DA层以外,还可以设计侧链DA层,通过锚定在主链的PoS链,PoS的验证人会对数据进行采样,然后将元数据传到L1,L1的交易可以通过cell_deps或者header_deps(看实现策略)读取commitment保证数据可用性。
虽然侧链存在一定的安全风险,但是参与该DA侧链网络的Layer2链越多,其安全保证就越大,因为有越多不可能合谋的参与方进来参与了采样。