0. 背景
- 双色球的玩法:
- 6个红球(1~33),1个蓝球(1~16)
- 中奖规则就是对红球和蓝球的匹配程度
- 双色球涉及现场开奖,需要一个可信任机构执行(由此也带来了黑幕的说法),违反了去中心化精神。
- 把类似双色球的玩法带入区块链,可以预见随着奖池的增大,将吸引越来越多的人参与。另外,如果计算机制不合理,可能导致某种程度上将趋近于黑洞——因为太难了,大家都中不了奖,奖池将无限累积——不过可以通过调整参数解决,或者就像PoW挖矿一样,奖池越大,吸引的算力越大。
1. 设想
- 整个流程只包括链下(浏览器)和链上两部分,不经过任何某个服务器。
2. 玩法
- 计算hash的内容模板:{slip0044-number}{serial-number}{serial-hash}{user-hash}{nounce}
- slip0044-number:slips/slip-0044.md at master · satoshilabs/slips · GitHub
- serial-number:每一期的期号,可以指定开始区块号和结束的区块号。
- serial-hash:每一期需要生成一个新的hash,防止抢跑。
- user-hash:用户支付费用后获取的凭证hash,防止冒名领取、重复领取。
- nounce: 客户端每次修改这部分计算出新hash,直到中奖,或者超时。
- 用户花费1000 CKB获得(比如)100 blocks的计算时间,返回user-hash。
- 用户在链下根据0中的内容规则,拼接字符长计算hash,找到符合规则的(见3中的两个方案),到链上发出请求兑奖,需要包含参数user-hash。
- 合约内部拼接字符床计算hash,再校验。如果符合进行转账,并返回一个新的user-hash。
3. 如何计算奖励
- kecaak256的hash是32个整数,取值范围0~255;
blake2b的hash是64个整数,取值范围0~255。 - 奖池包括初始奖池(来源见4),加卖票费用的80%(另外20%进入DAO)。
- 方案1:在hash中寻找N个 相同 的数,算作初始奖励。随着N的增加,奖励增加。
- 方案2:在hash中寻找N个 连续 的数,算作初始奖励。随着N的增加,奖励增加。
- 问题:如何设定N?也许可以考虑通过DAO的投票进行调节?
- 问题:无论N合不合理,都难以避免用户使用服务器甚至特殊设备计算hash(只要奖池足够大)。如何解决这个问题?如何防止彩票成为科学家的乐园?
4. 通过DAO实现创世奖池和创世期号的hash的初始化
- 发行10~100个NFT,每个售价M CKB。
- 销售费用的10%作为初始奖池,10%进入DAO,剩下的费用归给团队(如果有工具,可以锁定这些费用,随着功能的完善进行解锁)。
- 持有NFT的权益:
- 50%以上的地址签名(含时间戳)开启创世期号(以及后续生成新期号);汇集所有签名,生成当期的hash。
- vote to earn:参与投票的地址,每次投票可以均分DAO内资金的P%,每个地址上限不高于(比如)1000 CKB。
- 投票权。调整N值;合约升级,迁移奖池;……
5 中奖概率
- 双色球中奖概率: 6.71% —— 概率学角度分析双色球中奖概率 - 知乎 (zhihu.com)
- 六等奖:5.889%
- 五等奖:0.7758%
- 四等奖:0.0434%
- 三等奖:0.000914%
- 二等奖:0.0000846%
- 一等奖:0.0000056%
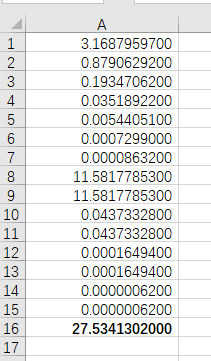
- 32个byte整数,出现3个相同数的概率:C(3,256) * P(29,256) / 256^32 = 3.16879597%
- 32个byte整数,出现4个相同数的概率:C(4,256) * P(28,256) / 256^32 = 0.87906292%
- 32个byte整数,出现5个相同数的概率:C(5,256) * P(27,256) / 256^32 = 0.19347062%
- 32个byte整数,出现6个相同数的概率:C(6,256) * P(26,256) / 256^32 = 0.03518922%
- 32个byte整数,出现7个相同数的概率:C(7,256) * P(25,256) / 256^32 = 0.00544051%
- 32个byte整数,出现8个相同数的概率:C(8,256) * P(24,256) / 256^32 = 0.00072990%
- 32个byte整数,出现9个相同数的概率:C(9,256) * P(23,256) / 256^32 = 0.00008632%
- 32个byte整数,出现长度为3的递增序列的概率:C(1,30) * 254 * 255 * 256^29 / 256^32 = 11.58177853%
- 32个byte整数,出现长度为4的递增序列的概率:C(1,29) * 254 * 255 * 256^28 / 256^32 = 0.04373328%
- 32个byte整数,出现长度为5的递增序列的概率:C(1,28) * 254 * 255 * 256^27 / 256^32 = 0.00016494%
- 32个byte整数,出现长度为6的递增序列的概率:0.00000062%
- 32个byte整数,出现长度为7的递增序列的概率:≈ 0
- 32个byte整数,出现长度为8的递增序列的概率:≈ 0
- 32个byte整数,出现长度为9的递增序列的概率:≈ 0
所以,相同数+递增序列+递减序列 = 相同数+递增序列 x2 ≈ 27.53413%
计算代码
6.0 实现:将长度64的hex字符串(blake2b、sha256)转换成长度为32的u8数组
// by ChatGPT 3.5
// not tested
fn main() {
let hex_string = "7355dd5276c21cfe0c593b5063b96af3f96a454b33216f58314f44c3ade92e9cd6cec4210a0836246780e9baf927cc50b9a3d7073e8f9bd12780fddbcb930c6d";
// Check if the input string is a valid hex string (only contains valid hex characters)
if hex_string.chars().all(|c| c.is_ascii_hexdigit()) {
let bytes = hex_string
.as_bytes()
.chunks(2)
.map(|chunk| {
u8::from_str_radix(std::str::from_utf8(chunk).unwrap(), 16)
.expect("Failed to parse hex to u8")
})
.collect::<Vec<u8>>();
if bytes.len() == 32 {
let mut result: [u8; 32] = [0; 32];
result.copy_from_slice(&bytes);
println!("{:?}", result);
} else {
println!("Hex string must have 64 characters (32 bytes).");
}
} else {
println!("Input is not a valid hex string.");
}
}
6.1 实现:检索array: [u8; 32]中出现的相同数的最多的那个及其次数
// by ChatGPT 3.5
// not tested
use std::collections::HashMap;
fn main() {
let array: [u8; 32] = [1, 2, 3, 2, 4, 5, 6, 3, 2, 7, 8, 9, 1, 4, 5, 6, 2, 3, 10, 11, 10, 12, 13, 14, 15, 12, 16, 17, 18, 19, 18, 20];
let mut counts = HashMap::new();
for &num in &array {
let count = counts.entry(num).or_insert(0);
*count += 1;
}
let (max_num, max_count) = counts.iter().max_by_key(|&(_, count)| count).unwrap();
println!("整数 {} 出现最多,共出现 {} 次", max_num, max_count);
}
6.2 实现:检索array: [u8; 32]中最长的那个递增/递减序列
// by ChatGPT 3.5
// not tested
fn find_longest_increasing_sequence(arr: &[u8], asc: bool) -> &[u8] {
let mut max_len = 0;
let mut current_len = 1;
let mut max_start = 0;
let mut current_start = 0;
for i in 1..arr.len() {
if asc && arr[i] > arr[i - 1] {
current_len += 1;
} else if !asc && arr[i] < arr[i - 1] {
current_len += 1;
} else {
if current_len > max_len {
max_len = current_len;
max_start = current_start;
}
current_len = 1;
current_start = i;
}
}
if current_len > max_len {
max_start = current_start;
}
&arr[max_start..max_start + max_len]
}
fn main() {
let array: [u8; 32] = [1, 2, 3, 2, 4, 5, 6, 3, 2, 7, 8, 9, 1, 4, 5, 6, 2, 3, 10, 11, 10, 12, 13, 14, 15, 12, 16, 17, 18, 19, 18, 20];
let longest_increasing_sequence = find_longest_increasing_sequence(&array, true);
println!("最长递增序列: {:?}", longest_increasing_sequence);
}