Introduction
People who have spent some time thinking about Bitcoin would probably understand the statement “every UTXO is a NFT”, however this concept can be taken even further to say “every sat is a NFT” (sat of course referring to “satoshi”, the smallest unit of BTC).
Credit to Casey and the Ordinals folks here, I am not certain how far they’ve taken their ideas around non-fungibility of satoshis but the seed of this idea was their ground-breaking work.
I am sure it seems odd to mint a NFT for every single unit of a cryptocurrency, but with the power of cryptography we can find some interest properties.
Before we get started you’ll have to understand what hashing is, there is an article we have here– What Is a Hash Function? .
Merkle trees
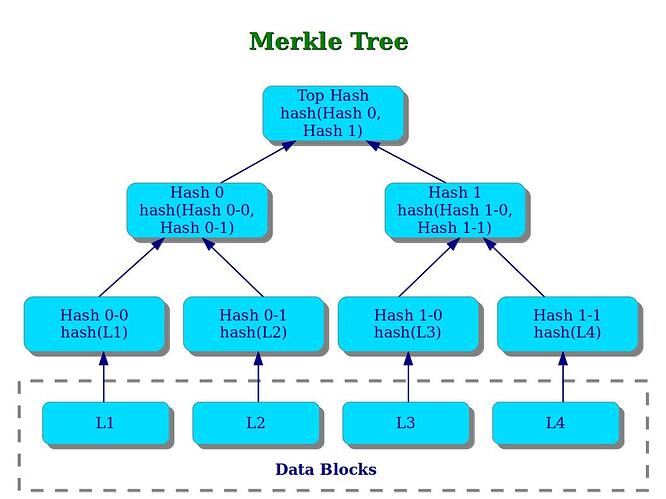
From here we will need to a Merkle tree, a data structure built out of hashed values. A tree of depth 2 can store 4 (2^2) values. A tree of depth 3 can store 8 (2^3) values. A tree of depth 8 can store 256 (2^8) values. I hope the trend is clear by now.
To build the tree we start at the lowest level with the values themselves, and hash together 2 items at a time to move to the next level of the tree. Item0 is hashed with Item1, Item2 is hashed with Item3, Item4 is hashed with Item5 and so on
As we climb to the next level of the tree, we will have a bunch of hashes (exactly 1/2 of the number of items) and we will repeat the process moving up the levels until we reach just 1 hash, the root hash, which can be used (along with additional proof data, the intermediary hashes which built the root) to prove the existence and integrity of any value that we started with.
Sparse Merkle trees
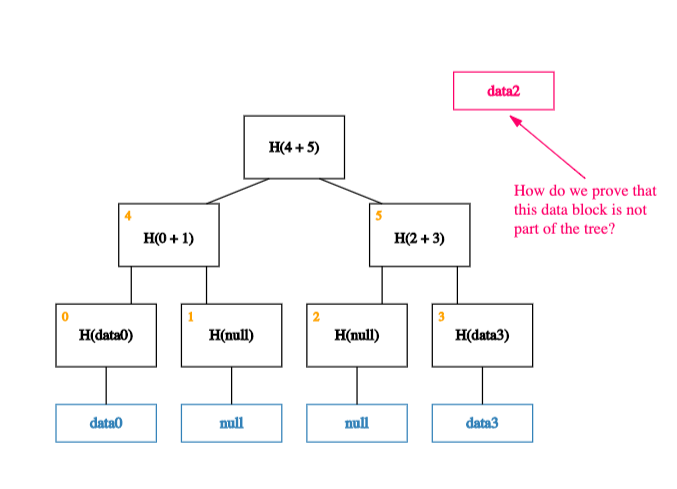
Now that we have built a Merkle tree, we will build a Sparse Merkle tree. This name is used because it is a Merkle tree that is filled with empty (0) values.
The unique thing about this tree is that because values are the same, when we hash them to build the tree, we will get the same results for each computation. For example, hashing Item0 with Item1 will produce the same output as hashing Item1 with Item2.
The impact of this fact is that we can calculate the root value of the tree by only doing 1 hash computation per level of the tree. We could find the root value of a sparse merkle tree with 256 values of (0) (depth of 8) with only 8 hash calculations, a sparse merkle tree with 512 values of (0) (depth of 9) with only 9 hash calculations.
Non-fungible sats
The base of our system will be a sparse merkle tree with sufficient depth for a value for each satoshi. Bitcoin enthusiasts will tell you that Satoshi chose the 21,000,000 BTC limit because 21,000,000 BTC * 100,000,000 satoshis gets close to the maximum of a 64 bit number. So we will choose a depth of 64 for our sparse merkle tree.
Each satoshi is effecitvely a NFT, we will set the value of each leaf in the merkle tree to an “owner address” who can spend the satoshi. When we hash all of the associated values of satoshi’s together, we will arrive at a root value containing the state of the system.
One simple trick
The insight that makes this system worth considering is that when we set all these leaves to the same owner address we get the same properties obseved when hashing together (0) values.
When we set the owner of a single satoshi, we will hash that value with itself and be able to set ownership of 2 consecutive satoshis, we can then hash the output of this with itself to set ownership of 4 consecutive satoshis, we can then hash the output of this with itself to set ownership of 8 consecutive satoshis.. and so on.
While the size of the Sparse merkle tree is enormous, managing it becomes reasonable because we are hashing duplicated values.
Spending these sats
In order to spend these sats, a single signature would be needed per owner address (the address would then be hashed the appropriate number of times to get the correct values to update the tree) or to compress the data needed here, we could prohibit address re-use and the transaction could contain only the binary positions the owner was spending.
It’s possible contract logic could be used instead of a simple address.
Like bills, which have denominations and can be broken up into smaller denominations, there’s a similar situation here in powers of 2 (x^2). Eventually we could end up with some stranded dust values that aren’t efficient to spend, but that is just part of a blockchain.
Conclusion
This system is neither UTXO or account, but has some properties of each. Like UTXO, ownership is asset-centric and transactions specify inputs and outputs.
Like account, an address can partially spend from their balance without moving the unspent coins, and the system naturally has a cryptographically authenticated global state.
I can see this being applicable to a novel kind of blockchain or Layer 2 design, or possibly being used in combination with a zk proof system.
I know there have been many takes (especially in the zk community) on using Merkle trees for blockchain state, if this idea is something that has been proposed before, I look forward to checking out your work!