Merkle Mountain Ranges are an amazingly efficient accumulator.
They only require storing tree roots which are a log of the number of elements in the data structure, and because they are formed with the same process as binary addition, their topology is contained in the binary representation of the number of elements in the structure.
Naively, the MMR root is a hash of the concatenation of the peaks (or a linked list of them), however this can be improved by recursing the peaks of the MMR into another MMR.
This process is repeated until only a single root remains.
Once the MMR is contained in a single root, the process can be restarted again, forming an endless heirarchy of MMR’s, inside a single MMR, with relatively efficient of proofs.
This does complicate proof generation, however, because each MMR is described by the size of its element set it should be straightforward to implement.
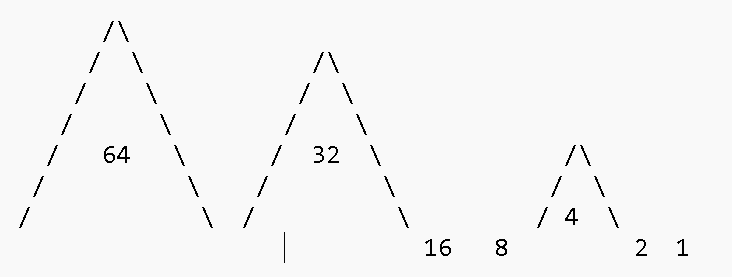
To demonstrate, suppose we have 100 transactions per block and 5 blocks to combine into a single data structure
First create an MMR for 100 transcations
100
0 1
0 2
1 4
0 8
0 16
1 32
1 64
create an MMR from the 3 peaks
3
1 1
1 2
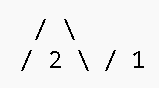
create an MMR from these 2 peaks
2
0 1
1 2
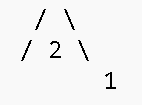
hashing these 2 peaks forms the MMR root, txRoot.
next take the 5 txRoot values to form a blockRoot (5 blocks)
5
1 1
0 2
1 4
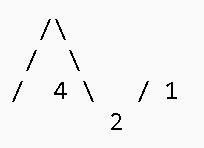
hash the 2 peaks that are left to form the MMR root, blockRoot
2
0 1
1 2
When adding to the MMR, it can be known which leaf values are needed through examining the previous number of elements and the number of elements to be added. You can see example code of this here: GitHub - matt-nervos/EfficientMMRinEVM